
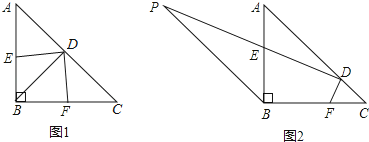
【题目】在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.、(1)如图1,若D为AC边上的中点.
(1)填空:∠C= ,∠DBC= ;
(2)求证:△BDE≌△CDF.
(3)如图2,D从点C出发,点E在PD上,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤1≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
【答案】(1)45°,45°;(2)见解析;(3)当t=0时,△PBE≌△CAE一对,当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对,当t=4时,△PBA≌△CAB一对.
【解析】
(1)利用等腰直角三角形的性质得出答案;
(2)利用等腰直角三角形的性质结合ASA进而得出答案;
(3)当t=0时,t=2时,t=4时分别作出图形,得出答案.
(1)解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,BD⊥AC,
∴∠DBC=45°;
故答案为:45°;45°;
(2)证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
∴BD⊥AC,
又∵ED⊥DF,
∴∠BDE+∠BDF=∠CDF+∠BDF=90°,
∴∠BDE=∠CDF,
∵∠C=∠DBC=45°,
∴BD=DC,∠EBD=90°-∠DBC=45°,
在△BDE和△CDF中,
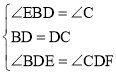 ,
,
∴△BDE≌△CDF(ASA);
(3)解:如图①所示:当t=0时,△PBE≌△CAE一对;
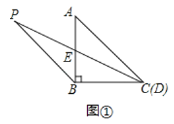
理由:∵BP∥AC
∴∠P=∠ACE
在△PBE和△CAE中,
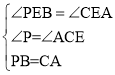
∴△PBE≌△CAE(AAS)
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对;
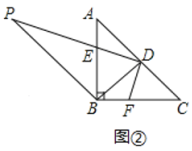
理由:在△ABD和△CBD中,
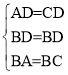
∴△ABD≌△CBD(SSS)
由(2)可知∠ADE+∠BDE=∠BDF+∠BDE,
∴∠ADE=∠BDF
在△AED和△BFD中,

∴△AED≌△BFD(ASA)
同理可证△BED≌△CFD.
如图③所示:当t=4时,△PBA≌△CAB一对.

理由:∵PB∥AC,
∴∠PBA=∠CAB,
在△PBA和△CAB中,

∴△PBA≌△CAB(SAS)
综上所述,答案为:
当t=0时,△PBE≌△CAE一对,当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对,当t=4时,△PBA≌△CAB一对.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点出发,按向上、向右、向下的方向依次不断移动,每次移动1个单位,其行走路线如下图,则A2019的坐标是( )

A.(2019,0)B.(504,0)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算,步骤如下:
①把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐;
②用被除式的第一项除以除式第一项,得到商式的第一项;
③用商式的第一项去乘除式,把积写在被除式下面(同类项对齐),消去相等项;
④把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止,被除式=除式×商式+余式.若余式为零,说明这个多项式能被另一个多项式整除.
例如:计算(6x4﹣7x3﹣x2﹣1)÷(2x+1),可用竖式除法如图:
所以6x4﹣7x3﹣x2﹣1除以2x+1,商式为3x3﹣5x2+2x﹣1,余式为0.
根据阅读材料,请回答下列问题(直接填空):

(1)(2x3+x﹣3)÷(x﹣1)= ;
(2)(4x2﹣4xy+y2+6x﹣3y﹣10)÷(2x﹣y+5)= ;
(3)[(x﹣2)(x﹣3)+1]÷(x﹣1)的余式为 ;
(4)x3+ax2+bx﹣15能被x2﹣2x+3整除,则a= ,b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
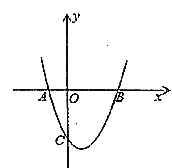
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连结AP和AQ,且BP=PQ=QC.求∠C的度数.
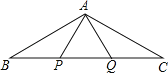
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA= ,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ= (等量代换)
∴△APQ是 三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠ .
又∵∠AQP是△AQC的外角,
∴∠AQP=∠ +∠ =60°.(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C= .
查看答案和解析>>
科目:初中数学 来源: 题型:
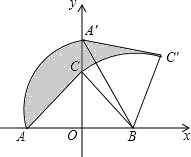
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
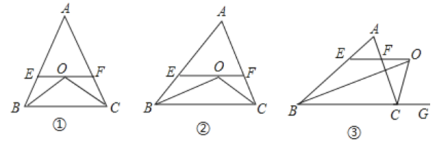
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图甲)和条形图(图乙),回答下列问题:
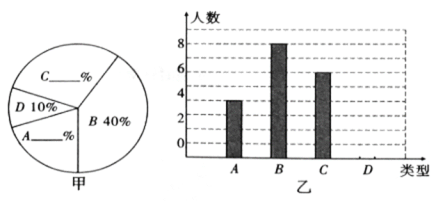
(1)求这次抽查的学生数;
(2)补全图甲和图乙;
(3)计算被抽查学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象过点A(4,1)与正比例函数
的图象过点A(4,1)与正比例函数![]() (
(![]() )的图象相交于点B(
)的图象相交于点B(![]() ,3),与
,3),与![]() 轴相交于点C.
轴相交于点C.
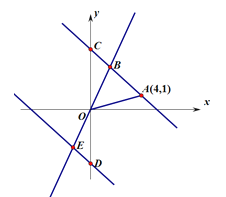
(1)求一次函数和正比例函数的表达式;
(2)若点D是点C关于![]() 轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
(3)在坐标轴上是否存在一点![]() ,使
,使![]() .若存在请求出点
.若存在请求出点![]() 的坐标,若不存在请说明理由.
的坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com