
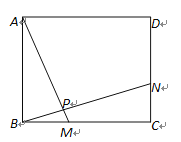
【题目】(1)如图1,已知正方形ABCD,点M和N分别是边BC,CD上的点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论;
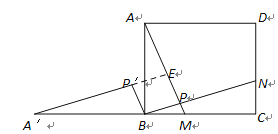
(2)如图2,将图(1)中的△APB绕着点B逆时针旋转90,得到△A′P′B,延长A′P′交AP于点E,试判断四边形BPEP′的形状,并说明理由.
【答案】(1)AM⊥BN,证明见解析;(2)四边形BPEP′是正方形,理由见解析.
【解析】
(1)易证△ABM≌△BCN,再根据角度的关系得到∠APB=90°,即可得到AM⊥BN;
(2)根据旋转的性质及(1)得到四边形BPEP′是矩形,再根据BP= BP′,得到四边形BPEP′是正方形.
(1)AM⊥BN
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠BCN=90°
∵BM=CN,
∴△ABM≌△BCN
∴∠BAM=∠CBN
∵∠CBN+∠ABN=90°,
∴∠ABN+∠BAM=90°,
∴∠APB=90°
∴AM⊥BN.
(2)四边形BPEP′是正方形.
△A′P′B是△APB绕着点B逆时针旋转90所得,
∴BP= BP′,∠P′BP=90.
又由(1)结论可知∠APB=∠A′P′B=90°,
∴∠BP′E=90°.
所以四边形BPEP′是矩形.
又因为BP= BP′,所以四边形BPEP′是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)读读做做:教材中有这样的问题,观察下面的式子,探索它们的规律,![]() =1-
=1-![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ……用正整数n表示这个规律是______;
……用正整数n表示这个规律是______;
(2)问题解决:一容器装有1L水,按照如下要求把水倒出:第一次倒出![]() L水,第二次倒出的水量是
L水,第二次倒出的水量是![]() L水的
L水的![]() ,第三次倒出的水量是
,第三次倒出的水量是![]() L水的
L水的![]() ,第四次倒出的水量是
,第四次倒出的水量是![]() L水的
L水的![]() ,……,第n+1次倒出的水量是
,……,第n+1次倒出的水量是![]() L水的
L水的![]() ,……,按照这种倒水方式,这1L水能否倒完?
,……,按照这种倒水方式,这1L水能否倒完?
(3)拓展探究:①解方程:![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
②化简:![]() +
+![]() +
+![]() …+
…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
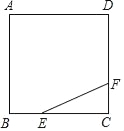
【题目】如图,正方形ABCD的边长为3,点E,F分别在边BCCD上,BE=CF=1,小球P从点E出发沿直线向点F运动,完成第1次与边的碰撞,每当碰到正方形的边时反弹,反弹时反射角等于入射角,则小球P与正方形的边第2次碰撞到__边上,小球P与正方形的边完成第5次碰撞所经过的路程为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
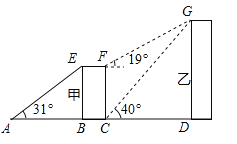
【题目】某学校教学楼(甲楼)的顶部E和大门A之间挂了一些彩旗.小颖测得大门A距甲楼的距离AB是31cm,在A处测得甲楼顶部E处的仰角是31°.
(1)求甲楼的高度及彩旗的长度;(精确到0.01m)
(2)若小颖在甲楼楼底C处测得学校后面医院楼(乙楼)楼顶G处的仰角为40°,爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为19°,求乙楼的高度及甲乙两楼之间的距离.(精确到0.01m)
(cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,对角线AC、BD交于点M.
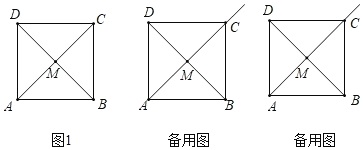
(1)直接写出AM= ;
(2)P是射线AM上的一点,Q是AP的中点,设PQ=x.
①AP= ,AQ= ;
②以PQ为对角线作正方形,设所作正方形与△ABD公共部分的面积为S,用含x的代数式表示S,并写出相应的x的取值范围.(直接写出,不需要写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,我们在2018年某月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”)该十字星的十字差为![]() ,再选择其它位置的十字星,可以发现“十字差”仍为48.
,再选择其它位置的十字星,可以发现“十字差”仍为48.
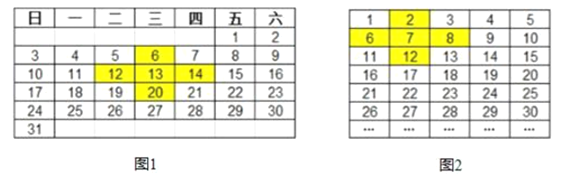
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
(2)若将正整数依次填入6列的长方形数表中,不同位置十字星的“十字差”是一个定值吗?如果是,请求出这个定值;如果不是,请说明理由.
(3)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数![]() 有关的定值,请用
有关的定值,请用![]() 表示出这个定值,并证明你的结论.
表示出这个定值,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com