练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知x=$\frac{2}{\sqrt{3}-1}$，求x2-x+1的值．

    分析 首先化简x=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1，进一步代入求得数值即可．

    解答 解：∵x=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1，
    ∴x2-x+1
    =（$\sqrt{3}$+1）2-（$\sqrt{3}$+1）+1
    =4+2$\sqrt{3}$-$\sqrt{3}$-1+1
    =4+$\sqrt{3}$．

    点评 此题考查二次根式的化简求值，注意先化简，再进一步代入求得数值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知a+$\frac{1}{a}$=$\sqrt{10}$，
    （1）求a2+$\frac{1}{{a}^{2}}$的值；
    （2）求a-$\frac{1}{a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列说法中，正确的个数是（　　）
    ①当k≠0时，y=$\frac{1}{kx}$是反比例函数；
    ②如果y=$\frac{1}{3{x}^{2}}$，那么y与x2成反比例；
    ③如果y=$\frac{m-1}{x}$+m2-1是反比例函数，则m=±1；
    ④如果x与y成正比例，y与z成反比例，则x与z成反比例．
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图△ABC中，AB=AC，BD是高，BD=6，DC=2，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在Rt△ABC中，∠C=90°，若a=12，c-a=8，求b，c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

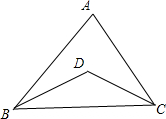    13．如图，BD，CD分别是△ABC的内角∠ABC、∠ACB的平分线，请说明∠BDC与∠A之间的等量关系是∠BDC=90°+$\frac{1}{2}$∠A．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：
    （1）（2+$\sqrt{5}$）10（2-$\sqrt{5}$）10；
    （2）（$\sqrt{3}$+$\sqrt{5}$-$\sqrt{6}$）（$\sqrt{3}$-$\sqrt{5}$-$\sqrt{6}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在雷达探测到的区域，可从建立平面直角坐标系来表示位置，在某次行动中，当我方两架飞机在A（-1，2）和B（3，2）的位置，可疑飞机在C（-1，-3）的位置，你能找出这个平面直角坐标系的横、纵坐标的轴的位置吗？把它们画出来，并确定可疑飞机的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图①，在矩形ABCD中，AB=6cm，BC=8cm，连结AC．动点P在线段AD上以4cm/s的速度从点D运动到点A．过点P作PK∥AC交DC于点K，以PK为边向下作正方形PEFK．设正方形PEFK与△ADC重叠部分图形面积为S（cm2），点P的运动时间为t（s）．
    （1）当EF落在线段AC上时，求t的值．
    （2）求S与t之间的函数关系式．
    （3）当正方形PEFK的顶点落在AB或BC边上时，求t的值．
    （4）如图②，点M在边AB上，且BM=2cm．另有一动点Q与点P同时出发，在线段BC上以4cm/s的速度从点B运动到点C．过点M、Q分别作AB、BC的垂线交于点N，得到矩形MBQN．当正方形PEFK与矩形MBQN重叠部分图形是四边形时，直接写出t的取值范围．

    查看答案和解析>>

    同步练习册答案