
 如图,已知A、B、C三点共线,OC、OE分别平分∠AOD、∠DOB.
如图,已知A、B、C三点共线,OC、OE分别平分∠AOD、∠DOB.分析 (1)根据OC、OE分别平分∠AOD、∠DOB,可知∠COE=90°;
(2)可设∠DOE=2x,∠COD=3x,然后根据图中的等量关系即可求出x的值.
解答 解:(1)∵OC、OE分别平分∠AOD、∠DOB,
∴∠COD=$\frac{1}{2}$∠AOD,∠DOE=$\frac{1}{2}$∠DOB,
∴∠COD+∠DOE=$\frac{1}{2}$(∠AOD+∠DOB)=90°;
(2)设∠DOE=2x,∠COD=3x,
由(1)可知:∠DOE+∠COD=90°,
∴2x+3x=90°,
∴x=18°,
∴∠DOE=36°,∠COD=54°,
∴∠COB=∠COD+2∠DOE=54°+72°=126°
点评 本题考查角的计算,涉及角平分线的性质,属于基础题型.


科目:初中数学 来源: 题型:解答题
 如图,△ABC的外角∠DAC的平分线AF交∠ABC的平分线BF于F,BF交AC于E,若∠BAC=80°,∠AEB:∠C=3:2,求∠F的度数.
如图,△ABC的外角∠DAC的平分线AF交∠ABC的平分线BF于F,BF交AC于E,若∠BAC=80°,∠AEB:∠C=3:2,求∠F的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在方格纸中,设单元格边长为1.
如图,△ABC在方格纸中,设单元格边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
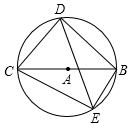 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
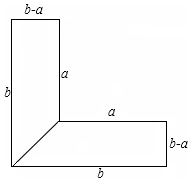 李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.
李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com