
 如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )
如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )| A、30° | B、40° |
| C、45° | D、60° |
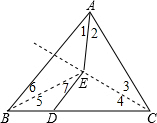 解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.
解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
| A、矩形的对角线相互垂直 |
| B、顺次连接平行四边形各边中点所得到的四边形是矩形 |
| C、等腰梯形的对角线互相垂直且相等 |
| D、对角线互相垂直平分的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=
如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC于点E.
如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC于点E.| 4 |
| 5 |
| OF |
| BD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据:
小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、可能事件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com