
【题目】某人驾车从A地到B地,出发2小时后车子出了点毛病,耽搁了半小时修车,为了弥补耽搁的时间他将车速增加到后来的1.6倍,结果按时到达,已知A、B两地相距100千米,求某人原来驾车的速度.
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.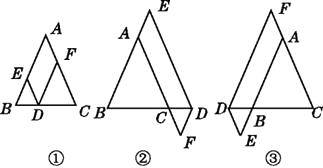
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有学生中,每班随机抽取6名学生,并对他们的数学学习情况进行了问卷调查,我们从调查的题目中特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A—非常喜欢”、“B—比较喜欢”、“C—不太喜欢”、“D—很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项而且只能选一项)结果进行统计.现将统计结果制成如下两幅不完整的统计图.请你根据以上提供的信息,解答下列问题:
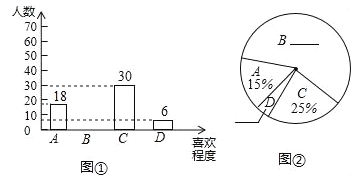
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取的学生对于数学学习喜欢程度的众数是:
(3)若该校七年级有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE ![]() AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为.
AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为.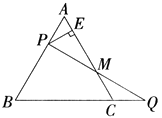
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角 ![]() ABC中,
ABC中, ![]() ACB=90
ACB=90 ![]() ,
, ![]() =60
=60 ![]() ,AD,CE分别是
,AD,CE分别是 ![]() BAC和
BAC和 ![]() BCA的平分线,AD,CE相交于点F.
BCA的平分线,AD,CE相交于点F.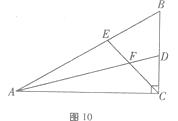
(1)求 ![]() EFD的度数;
EFD的度数;
(2)判FE与FD之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com