
【题目】如图,在直角 ![]() ABC中,
ABC中, ![]() ACB=90
ACB=90 ![]() ,
, ![]() =60
=60 ![]() ,AD,CE分别是
,AD,CE分别是 ![]() BAC和
BAC和 ![]() BCA的平分线,AD,CE相交于点F.
BCA的平分线,AD,CE相交于点F.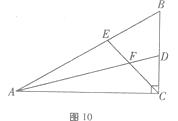
(1)求 ![]() EFD的度数;
EFD的度数;
(2)判FE与FD之间的数量关系,并证明你的结论.
【答案】
(1)解:如图所示,
∵在△ABC中,∠ACB=90°,∠B=60°,
∴∠BAC=30°
∵AD , CE分别是∠BAC和∠BCA的平分线,
∴∠FAC= ![]() ∠BAC=15°,∠FCA=
∠BAC=15°,∠FCA= ![]() ∠ACB=45°.
∠ACB=45°.
∴∠AFC=180°∠FAC∠FCA=120°,
∴∠EFD=∠AFC=120° 。
(2)解:结论:FE=FD.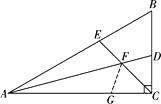
理由是:如图,在AC上截取AG=AE , 连接FG ,
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF.
在△AEF和△AGF中,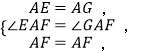
∴△AEF≌△AGF(SAS),
∴FE=FG , ∠AFE=∠AFG ,
∵∠EFD=120°,
∴∠DFC=60°,∠AFG=∠AFE=60°,
∴∠CFG=60°=∠DFC.
∵EC平分∠BCA ,
∴∠DCF=∠FCG=45°.
在△FGC和△FDC中,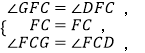
∴△FGC≌△FDC(ASA),
∴FG=FD ,
∴FE=FD.
【解析】(1)根据三角形的内角和得出∠BAC=30°,根据角平分线的定义得出∠FAC= ![]() ∠BAC=15°,∠FCA=
∠BAC=15°,∠FCA= ![]() ∠ACB=45°.根据三角形的内角和得出∠AFC=180°∠FAC∠FCA=120°,根据对顶角相等得出∠EFD=∠AFC=120°;
∠ACB=45°.根据三角形的内角和得出∠AFC=180°∠FAC∠FCA=120°,根据对顶角相等得出∠EFD=∠AFC=120°;
(2)结论:FE=FD.理由是:如图,在AC上截取AG=AE , 连接FG , 根据角平分线定义得出∠EAF=∠GAF.然后利用SAS判断出△AEF≌△AGF,然后根据全等三角形对应角相等,对应边相等得出FE=FG , ∠AFE=∠AFG , 根据邻补角的定义得出∠DFC=60°,∠AFG=∠AFE=60°,进而得出∠CFG=60°=∠DFC.根据角的角平分线的定义得出∠DCF=∠FCG=45°.然后利用ASA判断出△FGC≌△FDC,根据全等三角形对应边相等得出FG=FD , 根据等量代换得出答案。


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某人驾车从A地到B地,出发2小时后车子出了点毛病,耽搁了半小时修车,为了弥补耽搁的时间他将车速增加到后来的1.6倍,结果按时到达,已知A、B两地相距100千米,求某人原来驾车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm) | 150 | 155 | 160 | 163 | 165 | 168 |
人数(人) | 1 | 3 | 4 | 4 | 5 | 3 |
这组数据的众数是cm,中位数是cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,某公司的33名职工的月工资如下(单位:元):
职务 | 董事长 | 副董事长 | 总经理 | 董事 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5500 | 5000 | 3500 | 3230 | 2730 | 2200 | 1500 |
(1)该公司职工的月工资的平均数=元、中位数=元、众数=元.
(2)假设副董事长的工资从5 000元涨到15 000元,董事长的工资从5 500元涨到28 500元,那么新的平均工资=元、中位数=元、众数=元.(精确到1元)
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com