
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.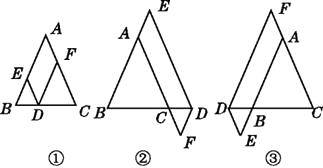
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
【答案】
(1)证明:∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠C,
∴∠FDC=∠C,∴DF=FC,
∴DE+DF=AF+FC=AC
(2)解:当点D在边BC的延长线上时,DE-DF=AC;
∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠ACB,
∴∠FDC=∠ACB,
∵∠DCF=∠ACB,
∴∠FDC=∠DCF
∴DF=FC,
∴AC+CF=AC+DF=AF=DE
DE-DF=AC;
同理可证当点D在边BC的反向延长线上时,DF-DE=AC
(3)2或10
【解析】(3)根据(1)的结论DE+DF=AC
∵AC=6,DE=4
∴DF=AC-DE=6-4=2
根据图②的结论DE-DF=AC
∴DF=DE-AC=-2,不符合题意;
根据图③的结论DF-DE=AC
∴DF=DE+AC=4+6=10
(1)根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠C,得到DF=FC,然后根据DE+DF=AF+FC,即可证得结论。
(2)图②根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠DCF,得到DF=FC,然后根据AC+CF=AC+DF=AF=DE,即可证得结论;同理可得出图③的结论。
(3)利用(1)(2)(3)的结论计算即可。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
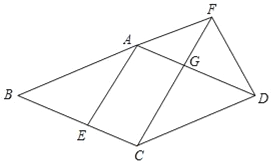
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
求证:(1)FD=CG;
(2)CG2=FGFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出三年以来,广东企业到“一带一路”国家投资越来越活跃,据商务部门发布的数据显示,2016年广东省对沿线国家的实际投资额超过4000000000美元,将4000000000用科学记数法表示为( )
A.0.4×109
B.0.4×1010
C.4×109
D.4×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(不要求写理由)
(3)在(2)的条件下,当∠DBA等于多少度时,存在AQ=2BD?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人驾车从A地到B地,出发2小时后车子出了点毛病,耽搁了半小时修车,为了弥补耽搁的时间他将车速增加到后来的1.6倍,结果按时到达,已知A、B两地相距100千米,求某人原来驾车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com