
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(不要求写理由)
(3)在(2)的条件下,当∠DBA等于多少度时,存在AQ=2BD?说明理由.
【答案】
(1)解:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中: 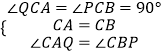 ,
,
∴△ACQ≌△BCP(ASA)
∴BP=AQ
(2)解:成立
(3)解:由(2)可知,BP=AQ,故要使AQ=2BD,需使BP=2BD,即需AB=AP,就需∠DBA=∠P,结合∠DBA+∠P=∠BAC=45°可知,只需∠DBA=22.5°即可
【解析】(1)利用ASA可证明△ACQ≌△BCP,从而证出结论;
(2)画出图形可得结论;
(3)由(2)知BP=AQ,又AQ=2BD,则BP=2BD,即AB=AP,由等腰三角形的性质可得∠DBA=∠P,又∠DBA+∠P=∠BAC=45°,可得出∠DBA的度数.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.
(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克.
①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.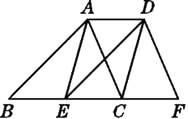
(1)求证:△ABC≌△DEF;
(2)试判断:四边形AECD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.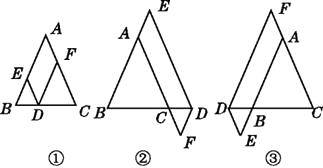
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com