
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.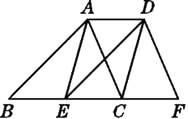
(1)求证:△ABC≌△DEF;
(2)试判断:四边形AECD的形状,并说明理由.
【答案】
(1)证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,
∴BC=EF.
在△ABC和△DEF中,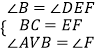
∴△ABC≌△DEF.
(2)解:四边形AECD是平行四边形.
理由:∵△ABC≌△DEF,∴AC=DF.
∵∠ACB=∠F,∴AC∥DF,
∴四边形ACFD是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,∴四边形AECD是平行四边形
【解析】(1)根据平行线的性质证出∠B=∠DEF.,再根据BE=EC=CF得出BC=EF,然后利用全等三角形的判定即可证得结论。
(2)根据全等三角形的性质得出AC=DF,再根据平行线的判定证明AC∥DF,可得到四边形ACFD是平行四边形,再根据平行四边形的性质得出AD∥CF,AD=CF,从而可证明AD=EC,然后再根据平行四边形的判定证得结论。


科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?( )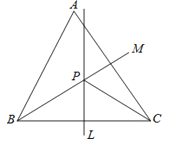
A.24°
B.30°
C.32°
D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于C点,D为抛物线的顶点,E为抛物线上一点,且C、E关于抛物线的对称轴对称,分别作直线AE、DE.
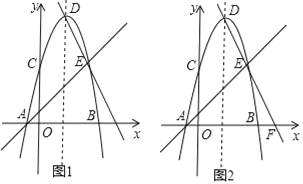
(1)求此二次函数的关系式;
(2)在图1中,直线DE上有一点Q,使得△QCO≌△QBO,求点Q的坐标;
(3)如图2,直线DE与x轴交于点F,点M为线段AF上一个动点,有A向F运动,速度为每秒2个单位长度,运动到F处停止,点N由F处出发,沿射线FE方向运动,速度为每秒![]() 个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值.
个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 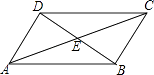
A.6
B.12
C.20
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出三年以来,广东企业到“一带一路”国家投资越来越活跃,据商务部门发布的数据显示,2016年广东省对沿线国家的实际投资额超过4000000000美元,将4000000000用科学记数法表示为( )
A.0.4×109
B.0.4×1010
C.4×109
D.4×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(不要求写理由)
(3)在(2)的条件下,当∠DBA等于多少度时,存在AQ=2BD?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017白银)据报道,2016年10月17日7时30分28秒,神舟十一号载人飞船在甘肃酒泉发射升空,与天宫二号在距离地面393000米的太空轨道进行交会对接,而这也是未来我国空间站运行的轨道高度.393000用科学记数法表示为( )
A.39.3×104
B.3.93×105
C.3.93×106
D.0.393×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com