
【题目】已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③3是方程ax2+2x+c=0的一个根;
④当﹣1<x<3时,ax2+2x+c>0
其中正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
先由抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),列方程组求出a,c,从而解得其解析式,进而求得其对称轴,再根据二次函数与方程和二次函数与不等式的关系可解.
把点(﹣1,﹣1),(0,3)代入y=ax2+3x+c得:![]()
∴![]()
∴y=﹣x2+3x+3
∴①ac<0正确;
该抛物线的对称轴为:![]() ,
,
∴②当x>1时,y的值随x值的增大而减小是错误的;
方程ax2+2x+c=0可化为:方程ax2+3x+c=x,
把x=3代入y=﹣x2+3x+3得y=3,
∴﹣x2+2x+3=0,
故③正确;
∴(3,3)在该抛物线上,
又∵抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),
∴抛物线y=ax2+3x+c与y=x的交点为(﹣1,﹣1)和(3,3),
当﹣1<x<3时,ax2+3x+c>x,即ax2+2x+c>0
④当﹣1<x<3时,ax2+2x+c>0,故④正确.
综上,①③④正确.
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
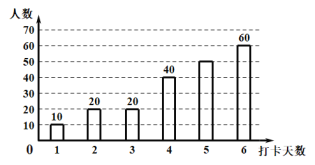
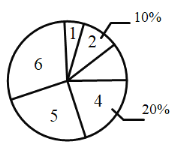
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
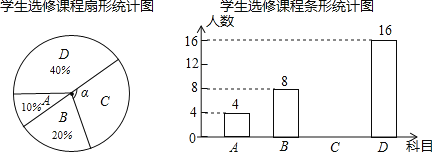
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读![]() 本书籍的人数所在扇形的圆心角度数是 ;
本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有![]() 名学生,估计该校在这次活动中阅读书籍的数量不低于
名学生,估计该校在这次活动中阅读书籍的数量不低于![]() 本的学生有多少人?
本的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:
![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是![]() ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;
(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为![]() ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C = 90°,以AC为直径的⊙O交AB于点D,连接OD,点E在BC上, B E=DE.

(1)求证:DE是⊙O的切线;
(2)若BC=6,求线段DE的长;
(3)若∠B=30°,AB =8,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com