
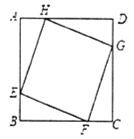
【题目】如图,在正方形![]() 的各边上顺次截取
的各边上顺次截取![]() ,若四边形
,若四边形![]() 面积是10,则正方形
面积是10,则正方形![]() 的面积为________.
的面积为________.
【答案】16
【解析】
利用SAS可证△AHE≌△BEF≌△CFG≌△DGH,从而证出四边形![]() 为正方形,然后利用勾股定理即可求出AH,从而求出AD,最后根据正方形的面积公式即可求出结论.
为正方形,然后利用勾股定理即可求出AH,从而求出AD,最后根据正方形的面积公式即可求出结论.
解:∵四边形ABCD为正方形
∴AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°
∵![]()
∴AH=BE=CF=DG
∴△AHE≌△BEF≌△CFG≌△DGH
∴EH=FE=GF=HG,∠AEH=∠BFE
∴四边形![]() 为菱形,
为菱形,
∵∠BFE+∠BEF=90°
∴∠AEH+∠BEF=90°
∴∠HEF=90°
∴四边形![]() 为正方形
为正方形
∵四边形![]() 面积是10,
面积是10,
∴![]()
∵AH2+AE2=![]()
∴AH2+32=![]()
解得:AH=1或-1(不符合实际,舍去)
∴AD=AH+HD=4
∴正方形![]() 的面积为
的面积为![]()
故答案为:16.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似地看作一次函数
(元)之间的关系可近似地看作一次函数![]() .物价部门规定该品牌的护眼灯售价不能超过36元.
.物价部门规定该品牌的护眼灯售价不能超过36元.
(1)如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?
(2)设该商店每月获得利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
(元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象和
的图象和![]() 都在第一象限内,
都在第一象限内,![]() ,
,![]() 轴,且
轴,且![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)若反比例函数![]() 的图象经过点B,求此反比例函数的解析式;
的图象经过点B,求此反比例函数的解析式;
(2)若将![]() 向下平移
向下平移![]() (m>0)个单位长度,
(m>0)个单位长度,![]() ,
,![]() 两点的对应点同时落在反比例函数图象上,求
两点的对应点同时落在反比例函数图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
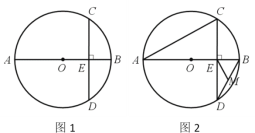
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
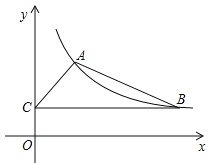
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,如果点![]() 到直线
到直线![]() 的距离与它到
的距离与它到![]() 轴、
轴、![]() 轴的距离都相等,那么称点
轴的距离都相等,那么称点![]() 为直线
为直线![]() 的“稳定点”.
的“稳定点”.
(1)到![]() 轴、
轴、![]() 轴的距离相等的点一定在直线__________________上;
轴的距离相等的点一定在直线__________________上;
(2)在下图中作出直线![]() ,并求出该直线所有“稳定点”的坐标;
,并求出该直线所有“稳定点”的坐标;
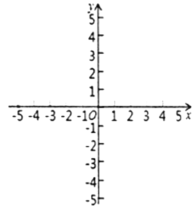
(备用图)
(3)当![]() 时,直线
时,直线![]() 的“稳定点”
的“稳定点”![]() 的坐标为__________________;
的坐标为__________________;
(4)当![]() 时,直线
时,直线![]() 的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降![]() 元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当
元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当![]() 为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
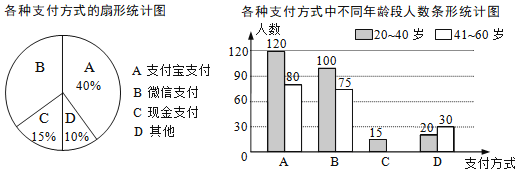
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③3是方程ax2+2x+c=0的一个根;
④当﹣1<x<3时,ax2+2x+c>0
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com