
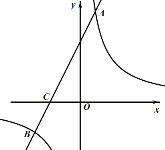
����Ŀ����ͼ��������y��ax2+bx+c��ͼ������A��1��0����B��3��0����C��0��3�����㣬����C��D����3��0����ֱ���������ߵ���һ����ΪE��
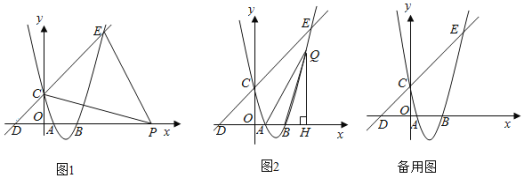
��1������ֱ��д����
�������ߵĽ���ʽ�� ����
��ֱ��CD�Ľ���ʽ�� ����
����E�����꣨�� ������ ������
��2����ͼ1������P��x����һ���㣬����PC��PE����Pλ�ںδ�ʱ����ʹ�á�CPE��45�㣬���������ʱ��P�����ꣻ
��3����ͼ2������Q����������һ���㣬��QH��x����H������QA��QB����QBƽ�֡�AQHʱ������ֱ��д����ʱ��Q�����꣮
���𰸡���1����y��x2��4x+3����y��x+3���ۣ�5��8������2��P1��1��0����P2��9��0������3��Q��3+![]() ��3+2
��3+2![]() ����
����
��������
��1�������������ߵĽ���ʽΪy��a��x��1����x��3������A��B���룬������������ߵĽ���ʽ��
����ֱ��CD�Ľ���ʽΪy��kx+b����C��D����ɵ�ֱ��CD�Ľ���ʽ��
��������������ʽ�ɵ�E�����ꣻ
��2������E��EH��x����H������֪���Ƴ�CD��![]() ��DE��
��DE��![]() ��EC��
��EC��![]() ����ECP�ס�EPD���ɴ˿ɵ�PE2�����ݹ��ɶ����ɵ�PH���ɴ˼��������P��������
����ECP�ס�EPD���ɴ˿ɵ�PE2�����ݹ��ɶ����ɵ�PH���ɴ˼��������P��������
��3���ӳ�QH��M��ʹ��HM��1������AM��BM���ӳ�QB��AM��N����Q��t��t2��4t+3����������õ�Qֻ���ڵ�B���Ҳ���������ϣ���QH��t2��4t+3��BH��t��3��AH��t��1���ɴ˿��Ƴ���QHB�ס�AHM���ݴ˿ɵ�QN��AM����BM��AB��2ʱ��QN��ֱƽ���߶�AM����ʱQBƽ�֡�AQH�����ݹ��ɶ����ɵ�tֵ�������Ƴ���Q���꣮
��1�����������߾���A��1��0����B��3��0����
����Լ��������ߵĽ���ʽΪy��a��x��1����x��3����
��C��0��3������õ�a��1��
�������ߵĽ���ʽΪy��x2��4x+3��
����ֱ��CD�Ľ���ʽΪy��kx+b������![]() ��
��
���![]() ��
��
��ֱ��CD�Ľ���ʽΪy��x+3��
����![]() �����
�����![]() ��
��![]() ��
��
��E��5��8����
�ʴ�Ϊ��y��x2��4x+3��y��x+3����5��8����
��2����ͼ1�У�����E��EH��x����H��
��C��0��3����D����3��0����E��5��8����
��OC��OD��3��EH��8��
���PDE��45�㣬CD��![]() ��DE��
��DE��![]() ��EC��
��EC��![]() ��
��
����CPE��45��ʱ���ߡ�PDE����EPC����CEP����PED��
���ECP�ס�EPD��
��![]() ��
��
��PE2��ECED��80��
��Rt��EHP��PH��![]() ��
��![]() ��4��
��4��
��ѵ�H���������ƽ��4����λ�õ���P��
��P1��1��0����P2��9��0����
��3���ӳ�QH��M��ʹ��HM��1������AM��BM���ӳ�QB��AM��N��

��Q��t��t2��4t+3����������õ�Qֻ���ڵ�B���Ҳ���������ϣ���QH��t2��4t+3��BH��t��3��AH��t��1��
��![]() ��
��![]() ��t��3��
��t��3��![]() ��
��
�ߡ�QHB����AHM��90�㣬
���QHB�ס�AHM��
���BQH����HAM��
�ߡ�BQH+��QBH��90�㣬��QBH����ABN��
���HAM+��ABN��90�㣬
���ANB��90�㣬
��QN��AM��
�൱BM��AB��2ʱ��QN��ֱƽ���߶�AM����ʱQBƽ�֡�AQH��
��Rt��BHM��BH��![]() ��
��![]() ��
��![]() ��
��
��t��3+![]() ��
��
��Q��3+![]() ��3+2
��3+2![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������Ч������ʡ�ٴ���Ŀ֮һ�Ĺ����������������������ߡ�ȫ�渴���������跽ͨ����������ʩ����ƣ��Ӵ��ʵ���Ͷ�����ֲ�ǰ�ڵ���Ĺ��������Ա�֤������Ŀ���ʵ�֡����������д����IJ�����Ҫ���䡣ij������������Ϊ8�֡�10�ֵĿ�����12����ȫ����������һ�ο�������110�ֲ�����
��1����ó�����������Ϊ8�֡�10�ֵĿ�������������
��2�����Ź��̵Ľ�չ���ó�����Ҫһ���������������165�֣�Ϊ��������ó������¹��������ֿ�����6����������������Ϊ8�ֵĿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y=![]() ��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
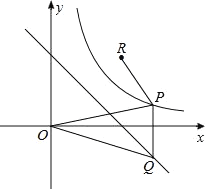

��1����ֱ��y=-x+2��������Χ�������ε��ܳ���
��2������PQO�����ΪS����S����Сֵ��
��3���趨��R��2��2�����Ե�PΪԲ�ģ�PRΪ�뾶����P�����P��ֱ��y=-x+2����M��N���㣮
���жϵ�Q���P��λ�ù�ϵ����˵�����ɣ�
����S��MON=S��PMNʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2m+1��x+m2��2��0��
��1�����÷���������ʵ��������m����С����ֵ��
��2�������̵�����ʵ����Ϊx1��x2���ң�x1��x2��2+m2��21����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
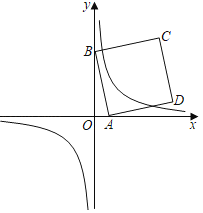
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��0��6����B��2��0����C��6��0����DΪ�߶�BC�ϵĶ��㣬��ADΪ�����Ҳ���������ADEF������CF��DE�ڵ�P����CP�����ֵ_____��
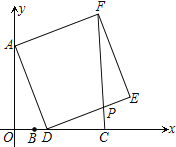
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() (
(![]() ��
��![]() )��ͼ���뷴��������
)��ͼ���뷴��������![]() (
(![]() )��ͼ����A��B���㣬��
)��ͼ����A��B���㣬��![]() �ύ��C�㣬��A������Ϊ(
�ύ��C�㣬��A������Ϊ(![]() ��6)����C������Ϊ(��2��0)����
��6)����C������Ϊ(��2��0)����![]() ��
��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����ꣻ
��3������ͼ����ʽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˿��Ƶĵ����ֱ���2��5��6��8����������ͬ�⣬�����ͬ��������ϴ�Ⱥ��泯�Ϸ�������
��1�������������ȡһ���ƣ��������Ƶĵ�����ż���ĸ���Ϊ�� ����
��2���������ȡһ���Ʋ��Żأ������ٳ�ȡһ���ƣ������б�������״ͼ����ֻѡ����һ�֣���ʾ�����п��ܳ��ֵĽ�����������������Ƶĵ�������ż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A������ΪA��1��0��������ֱ��������ABC�ı�AB��x����������ϣ���ABC��90������B�ڵ�A���Ҳ࣬��C�ڵ�һ���ޣ�����ABC�Ƶ�A��ʱ����ת75���������C�Ķ�Ӧ��Eǡ������y����������ϣ���ô��C������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������ͼ��Ľ������꣬��������������������ʽ��ɷ����飬������Ľ���ǽ�������꣮�磺��ֱ��y��2x+3��y����x+6�Ľ������꣬���ǿ���������������ʽ�õ�������![]() �����
�����![]() ������ֱ��y��2x+3��y����x+6�Ľ�������Ϊ��1��5��������������֪ʶ����������⣺
������ֱ��y��2x+3��y����x+6�Ľ�������Ϊ��1��5��������������֪ʶ����������⣺
��1����ֱ֪��y��kx��2��������y��x2��2x+3��
����k��4ʱ����ֱ���������ߵĽ������ꣻ
����kΪ��ֵʱ��ֱ����������ֻ��һ�����㣿
��2����֪��A��a��0����x���ϵĶ��㣬B��0��4![]() ������ABΪ����AB�Ҳ���������ABCD����������ABCD�ı��뷴��������y��
������ABΪ����AB�Ҳ���������ABCD����������ABCD�ı��뷴��������y��![]() ��ͼ����4������ʱ������a��ȡֵ��Χ��
��ͼ����4������ʱ������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com