
【题目】我们知道求函数图象的交点坐标,可以联立两个函数解析式组成方程组,方程组的解就是交点的坐标.如:求直线y=2x+3与y=﹣x+6的交点坐标,我们可以联立两个解析式得到方程组![]() ,解得
,解得![]() ,所以直线y=2x+3与y=﹣x+6的交点坐标为(1,5).请利用上述知识解决下列问题:
,所以直线y=2x+3与y=﹣x+6的交点坐标为(1,5).请利用上述知识解决下列问题:
(1)已知直线y=kx﹣2和抛物线y=x2﹣2x+3,
①当k=4时,求直线与抛物线的交点坐标;
②当k为何值时,直线与抛物线只有一个交点?
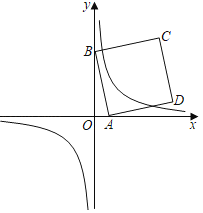
(2)已知点A(a,0)是x轴上的动点,B(0,4![]() ),以AB为边在AB右侧做正方形ABCD,当正方形ABCD的边与反比例函数y=
),以AB为边在AB右侧做正方形ABCD,当正方形ABCD的边与反比例函数y=![]() 的图象有4个交点时,试求a的取值范围.
的图象有4个交点时,试求a的取值范围.
【答案】(1)①(1,2),(5,18);②k=﹣2![]() ;(2)a的取值范围是a>2或﹣16<a<﹣4
;(2)a的取值范围是a>2或﹣16<a<﹣4
【解析】
(1)①由题意得: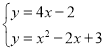 ,解得
,解得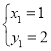 ,
, ,即可求解;
,即可求解;
②利用△=0,即可求解;
(2)分a>0、a<0两种情况,探讨正方形的边与反比例函数图象交点的情况,进而求解.
解:(1)①由题意得: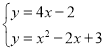 ,解得
,解得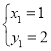 ,
, ,
,
∴直线与抛物线的交点坐标是(1,2),(5,18);
②联立两个函数并整理得:x2﹣(k+2)x+5=0,
△=(﹣k﹣2)2﹣4×5=0,
解得:k=﹣2![]() ;
;
(2)①当a>0时,如图1,
点A、B的坐标分别为:(a,0)、(0,4![]() ),
),
由点A、B的坐标得,直线AB的表达式为:y=﹣![]() x+4
x+4![]() ,
,
当线段AB与双曲线有一个交点时,
联立AB表达式与反比例函数表达式得:﹣![]() x+4
x+4![]() =
=![]() ,
,
整理得:4x2﹣4ax+2a=0,
△=(﹣4a)2﹣16×2a=0,解得:a=2,
故当a>2时,正方形ABCD与反比例函数的图象有4个交点;
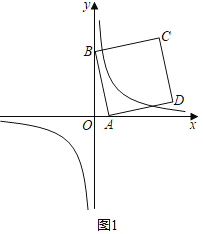
②当a<0时,如图2,
(Ⅰ)当边AD与双曲线有一个交点时,
过点D作ED⊥x轴于点E,
∵∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠ADE=∠BAO,
∵AB=AD,∠AOB=∠DEA=90°,
∴△AOB≌△DEA(AAS),
∴ED=AO=﹣a,AE=OB=4![]() ,
,
故点D(a+4![]() ,a),
,a),
由点A、D的坐标可得,直线AD的表达式为:y=![]() a(x﹣a),
a(x﹣a),
联立AD与反比例函数表达式并整理得:ax2﹣a2x﹣16=0,
△=(﹣a2)2﹣4a×(16)=0,解得:a=﹣4(不合题意值已舍去);
(Ⅱ)当边BC与双曲线有一个交点时,
同理可得:a=﹣16,
所以当正方形ABCD的边与反比例函数的图象有4个交点时,a的取值范围为:﹣16<a<﹣4;
综上所述,a的取值范围是a>2或﹣16<a<﹣4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象,经过点A(1,0),B(3,0),C(0,3)三点,过点C,D(﹣3,0)的直线与抛物线的另一交点为E.
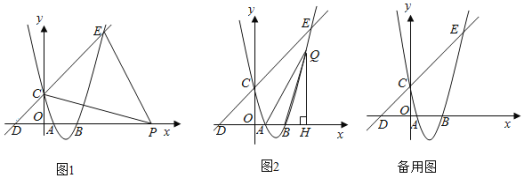
(1)请你直接写出:
①抛物线的解析式 ;
②直线CD的解析式 ;
③点E的坐标( , );
(2)如图1,若点P是x轴上一动点,连接PC,PE,则当点P位于何处时,可使得∠CPE=45°,请你求出此时点P的坐标;
(3)如图2,若点Q是抛物线上一动点,作QH⊥x轴于H,连接QA,QB,当QB平分∠AQH时,请你直接写出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设一次函数y=ax+b(a,b是常数,且a≠0)的图象A(1,3)和B(-1,-1)两点.
(1)求该一次函数的表达式.
(2)①若点(![]() ,2)在(1)中的函数图象上,求m的值.
,2)在(1)中的函数图象上,求m的值.
②若(1)中的函数图象和y=-2x+n的函数图象的交点在第一象限,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=![]() ,AD=2cm,AB=4cm,BC=6cm,点E是CD中点,过点B画射线BF交CD于点F,交AD延长线于点G,且∠GBE=∠CBE,则线段DG的长为__cm.
,AD=2cm,AB=4cm,BC=6cm,点E是CD中点,过点B画射线BF交CD于点F,交AD延长线于点G,且∠GBE=∠CBE,则线段DG的长为__cm.
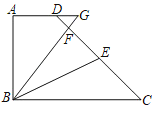
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区中学生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示尚不完整的统计图.
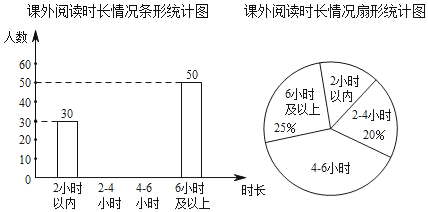
(1)本次调查共随机抽取了 名中学生,其中课外阅读时长“2~4小时”的有 人;
(2)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 °;
(3)若该地区共有20000名中学生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
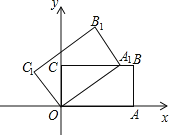
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标分别是
的坐标分别是![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 在第一、二象限的抛物线上,过点
在第一、二象限的抛物线上,过点![]() 作
作![]() 轴的平行线分别交
轴的平行线分别交![]() 轴和直线
轴和直线![]() 于点
于点![]() 、
、![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() .
.
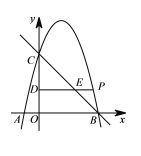
⑴求这条抛物线对应的函数表达式;
⑵当点![]() 在第一象限的抛物线上时,求
在第一象限的抛物线上时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
⑶在⑵的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
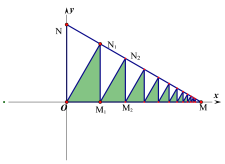
【题目】在平面直角坐标系中,直线![]() 与两坐标轴分别交于M、N两点,过点O作
与两坐标轴分别交于M、N两点,过点O作![]() ,过
,过![]() 作
作![]() ,得阴影
,得阴影![]() ;再过
;再过![]() 作
作![]() ,过
,过![]() 作
作![]() ,得阴影
,得阴影![]() ;……如此进行下去,则得到的所有阴影三角形的面积之和为_________.
;……如此进行下去,则得到的所有阴影三角形的面积之和为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com