
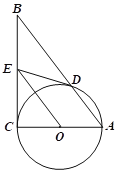
【题目】如图在RtΔABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,求△ADO的面积.
【答案】(1)答案见解析;(2)5;(3)1.08.
【解析】
(1)连OD,首先证明△EOC≌△EOD,则可以证得∠EDO=∠ECO=90°,即可证得;
(2)证明OE是△ABC的中位线,在直角△OEC中,利用勾股定理求得OE的长,然后利用三角形中位线定理求得AB的长;
(3)连接CD,则CD是直角△ABC的斜边AB上的高,根据三角形的面积公式即可求得CD的长,则在直角△ACD中,利用勾股定理求得AD的长,则可求出△ACD的面积,进而求得△ADO的面积.
(1)连OD.
∵OE∥AB,∴∠EOC=∠A,∠EOD=∠ODA.
又∵OA=OD,∴∠A=∠ODA,∴∠EOC=∠EOD.
在△EOC和△EOD中,∵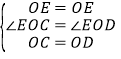 ,∴△EOC≌△EOD(SAS),∴∠EDO=∠ECO.
,∴△EOC≌△EOD(SAS),∴∠EDO=∠ECO.
又∵∠ECO=90°,∴∠EDO=90°即ED⊥DO 而点D在⊙O上,∴ED为⊙O的切线.
(2)∵OE∥AB,OA=OC,∴AB=2OE.
在△OCE中,OE=![]()
![]() ,∴AB=2OE=5;
,∴AB=2OE=5;
(3)连结CD.
∵AC=2OA=3,AB=5,∴BC=![]() =
=![]() =4.
=4.
∵AC是⊙O的直径,∴∠CDA=90°,∴CD⊥AB.
在Rt△ABC中,CD⊥AB,∴CDAB=ACBC,∴CD=2.4.
在Rt△ACD中,AD=![]() =
=![]() =1.8,∴S△ACD=
=1.8,∴S△ACD=![]() CDAD=2.16,∴S△ADO=
CDAD=2.16,∴S△ADO=![]() S△ACD=1.08.
S△ACD=1.08.


科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
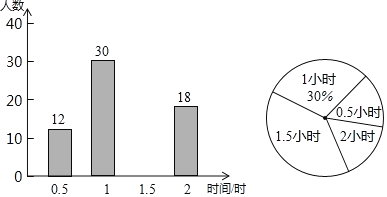
【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小游在九寨沟开店做牛肉生意,根据协议,每天他会用![]() 元购进牦牛肉和费牛肉
元购进牦牛肉和费牛肉![]() 斤,其中牦牛肉和黄牛肉的数量之比为
斤,其中牦牛肉和黄牛肉的数量之比为![]() ,已知每斤牦牛肉的售价比每斤黄牛肉的售价多
,已知每斤牦牛肉的售价比每斤黄牛肉的售价多![]() 元,预计当天可全部售完.
元,预计当天可全部售完.
(1)若小游预计每天盈利不低于![]() 元,则牦牛肉每斤至少卖多少元?
元,则牦牛肉每斤至少卖多少元?
(2)若牦牛肉和黄牛肉均在(1)的条件下以最低价格销售,但8月份因为九寨沟地震,游客大量减少,导致牛肉滞销,小游决定降价销售每天进购的牛肉,已知牦牛肉的单价下降![]() (其中
(其中![]() ) ,但销量还是比进购数量下降了
) ,但销量还是比进购数量下降了![]() ,黄牛肉每斤下降了
,黄牛肉每斤下降了![]() 元,销量比进购数量下降了
元,销量比进购数量下降了![]() ,最终每天牦牛肉的销售额比黄牛肉销售额的
,最终每天牦牛肉的销售额比黄牛肉销售额的![]() 倍还多
倍还多![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有( )
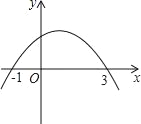
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
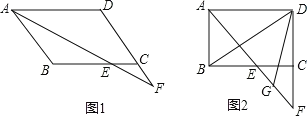
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中说明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com