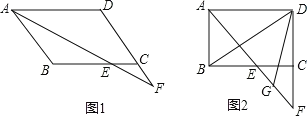
【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．
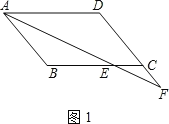
（1）在图1中说明CE=CF；
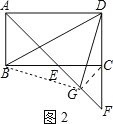
（2）若∠ABC=90°，G是EF的中点(如图2)，求∠BDG的度数．
【答案】（1）答案见解析；（2）∠BDG=45°．
【解析】
（1）先根据角平分线的定义可得
，再根据平行四边形的性质、平行线的性质可得
，从而可得
，然后根据等腰三角形的性质即可得证；
（2）先根据矩形的性质和题（1）的结论可得出
为等腰直角三角形，再根据等腰三角形的性质可得
，然后根据角平分线的定义、等腰三角形的判定与性质可得
，从而可得
，最后根据三角形全等的判定定理与性质可得
，从而可推出
为等腰直角三角形，由此即可得出答案．
（1）如图1，AF平分
∵四边形ABCD是平行四边形
；
（2）如图2，连接GC、BG
∵四边形ABCD为平行四边形，
∴四边形ABCD为矩形
结合（1）的结论得，为等腰直角三角形
∵G为EF中点
（等腰三角形的三线合一）
又
AF平分，
为等腰直角三角形，
，即
在
与
中，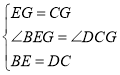
为等腰直角三角形
．
全优点练单元计划系列答案科目：初中数学 来源： 题型：
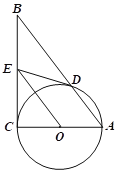
【题目】如图在RtΔABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过O作OE∥AB，交BC于E．
（1）求证：ED是⊙O的切线；
（2）如果⊙O的半径为1.5，ED=2，求AB的长．
（3）在（2）的条件下，求△ADO的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．
（1）问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；
（2）求原来的路线AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
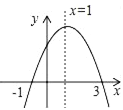
【题目】如图为二次函数y=ax2+bx+c的图象，给出下列说法：
①ab＞0；
②方程ax2+bx+c=0的根为x1=﹣1，x2=3；
③a+b+c＞0；
④当x＞1时，随x值的增大而增大．
其中正确的说法有______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解答下列各题
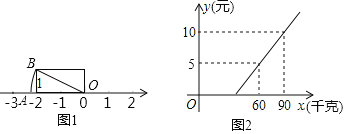
（1）如图1，已知OA＝OB，数轴上的点A所表示的数为m，且|m+n|＝2
①点A所表示的数m为 ；
②求代数式n2+m﹣9的值．
（2）旅客乘车按规定可以随身携带一定质量的行李，如果超过规定，则需购买行李票，设行李票y（元）是行李质量x（千克）的一次函数，其图象如图2所示．
①当旅客需要购买行李票时，求出y与x之间的函数关系式；
②如果张老师携带了42千克行李，她是否要购买行李票？如果购买需买多少行李票？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点F运动时，△FBC的面积y（cm2）随时间x（s）变化的关系图象，则a的值为（ ）
A. 
B. 2 C. 
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
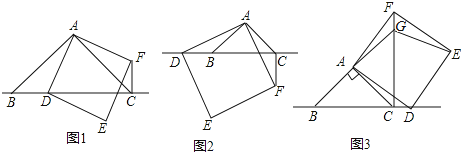
【题目】在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系，
②BC，CD，CF之间的数量关系为；
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；
若不成立，请你写出正确结论再给予证明；
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2
，CD=
BC，求CF，EG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
