
 如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.分析 (1)由弦切角定理可知∠PCA=∠B,由直角所对的圆周角等于90°可知∠ACB=90°.由同角的余角相等可知∠AED=∠B,结合对顶角的性质可知∠PCE=∠PEC;
(2)过点P作PF⊥AC,垂足为F.由锐角三角函数的定义和勾股定理可求得AC=8,AE=$\frac{5}{2}$,由等腰三角形三线合一的性质可知EF=$\frac{11}{4}$,然后证明△AED∽△PEF,由相似三角形的性质可求得PE的长,从而得到PC的长.
解答 解:(1)∵PC是圆O的切线,
∴∠PCA=∠B.
∵AB是圆O的直径,
∴∠ACB=90°.
∴∠A+∠B=90°.
∵PD⊥AB,
∴∠A+∠AED=90°.
∴∠AED=∠B.
∵∠PEC=∠AED,
∴∠PCE=∠PEC.
(2)如图所示,过点P作PF⊥AC,垂足为F.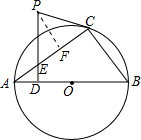
∵AB=10,sinA=$\frac{3}{5}$,
∴BC=AB•$\frac{3}{5}$=6.
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8.
∵DE=$\frac{3}{2}$,sinA=$\frac{3}{5}$,
∴AE=$\frac{5}{2}$.
∴EC=AC-AE=8-$\frac{5}{2}$=$\frac{11}{2}$.
∵PC=PE,PF⊥EC,
∴EF=$\frac{1}{2}EC=\frac{11}{4}$.
∵∠AED=∠PEF,∠EDA=∠EFP,
∴△AED∽△PEF.
∴$\frac{AE}{ED}=\frac{PE}{EF}$,$\frac{\frac{5}{2}}{\frac{3}{2}}=\frac{EP}{\frac{11}{4}}$.
解得:EP=$\frac{55}{12}$.
∴PC=$\frac{55}{12}$.
点评 本题主要考查的是切线的性质、圆周角定理、锐角三角函数的定义、勾股定理、相似三角形的性质和判定、等腰三角形的性质,证得△AED∽△PEF是解题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (0,0) | C. | (-1,-1) | D. | (-2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x+1}$ | B. | $-\frac{1}{x+1}$ | C. | $-\frac{1}{x-1}$ | D. | $\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{2}$,3 | B. | $\sqrt{2}$,$\sqrt{3}$,5 | C. | 1.5,2,2.5 | D. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
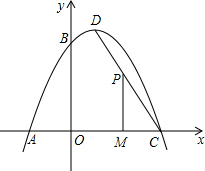 如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
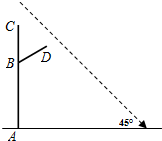 如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com