
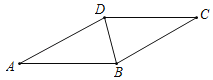
【题目】如图,BD是菱形ABCD的对角线,∠CBD=75°.
(1)求∠A的度数;
(2)请用尺规作图,在AD边上找到一点F,使得∠DBF=45°(不要求写作法,保留作图痕迹)
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA,求抛物线的解析式( )
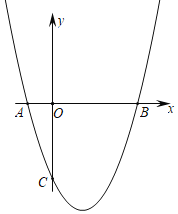
A.y=x2﹣2x﹣3B.y=x2﹣2x+3C.y=x2﹣2x﹣4D.y=x2﹣2x﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
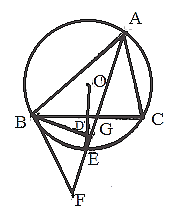
【题目】如图,点E为△ABC的外接圆⊙O上一点,OE⊥BC于点D,连接AE并延长至点F,使∠FBC=∠BAC,
(1)求证:直线BF是⊙O的切线;
(2)若点D为OE中点,过点B作BG⊥AF于点G,连接DG,⊙O的半径为![]() ,AC=5.
,AC=5.
①求∠BAC的度数;
②求线段DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,E为⊙O上一点,C为弧BE的中点,过点C作AE的垂线,交AE的延长线于点D.

(1)求证:CD是⊙O的切线;
(2)连接EC,若AB=10,AC=8,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
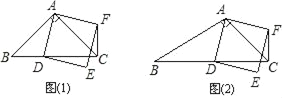
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△OAB绕O点逆时针旋转60°得到△OCD,若OA=4,∠AOB=35°,则下列结论错误的是( )
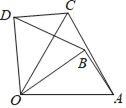
A. ∠BDO=60° B. ∠BOC=25° C. OC=4 D. BD=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学去年举办竞赛,颁发一二三等奖各若干名,获奖人数依次增加,各获奖学生获得的奖品价值依次减少(奖品单价都是整数元),其中有3人获得一等奖,每人获得的奖品价值34元,二等奖的奖品单价是5的倍数,获得三等奖的人数不超过10人,并且获得二三等奖的人数之和与二等奖奖品的单价相同.今年又举办了竞赛,获得一二三等奖的人数比去年分别增加了1人、2人、3人,购买对应奖品时发现单价分别上涨了6元、3元、2元.这样,今年购买奖品的总费用比去年增加了159元.那么去年购买奖品一共花了__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
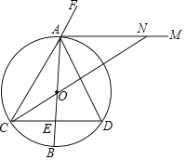
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD外角∠DAF的平分线.
(1)求证:AM是⊙O的切线.
(2)若C是优弧ABD的中点,AD=4,射线CO与AM交于N点,求ON的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com