
【题目】如图,AB为⊙O的直径,E为⊙O上一点,C为弧BE的中点,过点C作AE的垂线,交AE的延长线于点D.

(1)求证:CD是⊙O的切线;
(2)连接EC,若AB=10,AC=8,求△ACE的面积.
【答案】(1)见解析;(2)△ACE的面积=![]() .
.
【解析】
(1)连接OC,由C为弧BE的中点,得到![]() ,求得∠CAD=∠BAC,根据等腰三角形的性质得到∠BAC=∠ACO,推出AD∥OC,根据平行线的性质得到OC⊥CD,于是得到CD是⊙O的切线;
,求得∠CAD=∠BAC,根据等腰三角形的性质得到∠BAC=∠ACO,推出AD∥OC,根据平行线的性质得到OC⊥CD,于是得到CD是⊙O的切线;
(2)连接BC,根据圆周角定理得到∠ACB=90°,根据勾股定理得到BC=![]() ,根据相似三角形的性质和三角形的面积公式即可得到结论.
,根据相似三角形的性质和三角形的面积公式即可得到结论.
(1)证明:连接OC,

∵C为弧BE的中点,
∴![]() ,
,
∴∠CAD=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO,
∴∠CAD=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连接BC,

∵AB为⊙O的直径,
∴∠ACB=90°,
∵AB=10,AC=8,
∴BC=![]() ,
,
∵∠D=∠ACB=90°,
∠DAC=∠CAB,
∴△ACD∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,CD=
,CD=![]() ,
,
∵![]()
∴CE=BC=6,
∴DE=![]() ,
,
∴AE=AD﹣DE=![]() ,
,
∴△ACE的面积=![]() AECD=
AECD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=6,BC=4,点E在边AB上(不与点A、B重合),过点D作DF⊥DE,交边BC的延长线于点F.
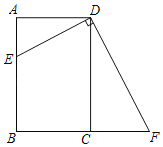
(1)求证:△DAE∽△DCF.
(2)设线段AE的长为x,线段BF的长为y,求y与x之间的函数关系式.
(3)当四边形EBFD为轴对称图形时,则cos∠AED的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c开口向上,与x轴交于点A、B,与y轴交于点C
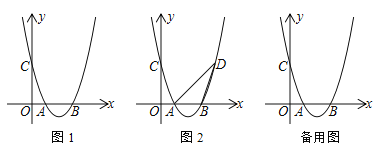
(1) 如图1,若A (1,0)、C (0,3)且对称轴为直线x=2,求抛物线的解析式
(2) 在(1)的条件下,如图2,作点C关于抛物线对称轴的对称点D,连接AD、BD,在抛物线上是否存在点P,使∠PAD=∠ADB,若存在,求出点P的坐标,若不存在,请说明理由
(3) 若直线l:y=mx+n与抛物线有两个交点M、N(M在N的左边),Q为抛物线上一点(不与M、N重合),过点Q作QH平行于y轴交直线l于点H,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美武汉·诗意江城”,某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校3000名学生中的部分学生,提供四个景点选择:A、黄鹤楼;B、东湖海洋世界;C、极地海洋世界;D、欢乐谷.要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
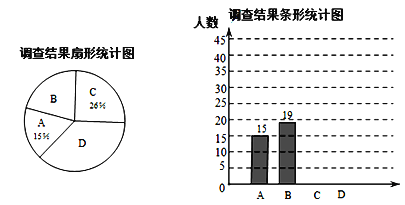
请根据图中提供的信息,解答下列问题:
(1) 一共调查了学生___________人
(2) 扇形统计图中表示“最想去的景点D”的扇形圆心角为___________度
(3) 如果A、B、C、D四个景点提供给学生优惠门票价格分别为20元、30元、40元、60元,根据以上的统计估计全校学生到对应的景点所需要门票总价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒,若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长,设剪去的小正方形边长是xcm,根据题意可列方程,化为一般式为_____.
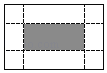
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是菱形ABCD的对角线,∠CBD=75°.
(1)求∠A的度数;
(2)请用尺规作图,在AD边上找到一点F,使得∠DBF=45°(不要求写作法,保留作图痕迹)
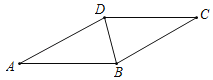
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 拼合在一个平面上,边
拼合在一个平面上,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 方向滑动.当点
方向滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,点
时,点![]() 运动的路径长为______
运动的路径长为______![]() .
.
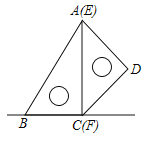
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
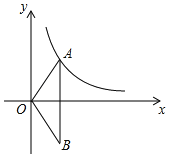
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com