
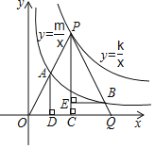
【题目】如图,在第一象限内,动点P在反比例函数y=![]() 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=
的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=![]() 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
①![]() 为定值;②若k=4m,则A为OP中点;③S△PEB=
为定值;②若k=4m,则A为OP中点;③S△PEB=![]() ;④OA2+PB2=PQ2.
;④OA2+PB2=PQ2.
A.4B.3C.2D.1
【答案】A
【解析】
根据反比例函数系数k的几何意义和等腰三角形的性质,相似三角形的性质即可判断.
解:①正确.∵A在反比例函数![]() 的图象上,P在反比例函数
的图象上,P在反比例函数![]() 的图象上,
的图象上,
∴S△AOD=![]() |m|,S△poc=
|m|,S△poc=![]() |k|,
|k|,
∵PC⊥OQ于点C,AD⊥OQ于点D,
∴AD∥PC,
∴△AOD∽△POC,
∴ 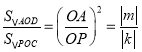 ,
,
∴ ![]() 为定值,
为定值,
∵△OPQ是以P为顶点的等腰三角形,
∴OP=PQ,
∴![]() 为定值;故此选项正确; ②正确,
为定值;故此选项正确; ②正确,
∵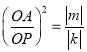 ,k=4m,
,k=4m,
∴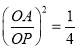 ,
,
∴ ![]() ,故此选项正确;
,故此选项正确;
③正确,延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ, ∴S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE=![]() m,
m,
∵S△PCQ=S△POC=![]() k,
k,
∴S△PEB=S△PCQ-S四边形CQBE=![]() k
k![]() m=
m=![]() ,故此选项正确; ④正确,
,故此选项正确; ④正确,
∵BE∥OQ,
∴△PEB∽∽△PCQ,
∴ 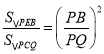 ,
,
∵S△PCQ=![]() k,S△PEB=
k,S△PEB=![]() ,
, 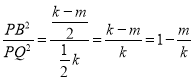 ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴OA2+PB2=PQ2,故此选项正确. 综上,选项正确的个数为4个 故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②3a+c=0;③ax2+bx≤a+b;④若M(﹣0.5,y1)、N(2.5,y2)为函数图象上的两点,则y1<y2.其中正确的是( )
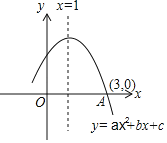
A.①③④B.①②3④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(﹣1,m)是双曲线y=![]() 上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.
上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.

(1)求m的值和双曲线对应的函数表达式;
(2)若经过点P的一次函数y=kx+b(k≠0、b≠0)的图象与x轴交于点A,与y交于点B且PB=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校学生每天体育锻炼所用时间情况,采用问卷的方式对一部分学生进行调查确定调查对象时,大家提出以下几种方案:(A)对各班体育委员进行调査;(B)对某班的全体学生进行调查;(C)从全校每班随机抽5名学生进行调查在问卷调查时,每位被调查的学都选择了问卷中适合自己的十个时间段,学生会将收集到的数据整理后续制成如下的统计表:
被调查的学生每天体育锻炼所用时间统计表
组别 | 时间x(小时) | 频数 |
一 | 0≤x≤0.5 | 15 |
二 | 0.6<x≤1 | 27 |
三 | 1<x≤1.5 | 38 |
四 | 1.5<x≤2 | 13 |
五 | x>2 | 7 |
(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案 (填A、B或C);
(2)被调查的学生每天体育锻炼所用时间的中位数落在 组;
(3)根据以上统计结果,估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数,并根据你计算的结果提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 是坐标原点,直线
是坐标原点,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 、
、![]() 两点.
两点.

(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为顶点的抛物线
为顶点的抛物线![]() 与直线
与直线![]() 的另一交点为
的另一交点为 ![]() (如图1),连
(如图1),连![]() 、
、![]() ,在点
,在点![]() 的运动过程中
的运动过程中![]() 的面积
的面积![]() 是否变化,若变化,求出
是否变化,若变化,求出![]() 的范围;若不变,求出
的范围;若不变,求出![]() 的值;
的值;
(3)平移(2)中的抛物线,使顶点为![]() ,抛物线与
,抛物线与![]() 轴的正半轴交于点
轴的正半轴交于点![]() (如图2) ,
(如图2) ,![]() ,
,![]() 为抛物线上两点,若以
为抛物线上两点,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求直线
,求直线![]() 经过的定点
经过的定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
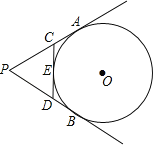
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com