
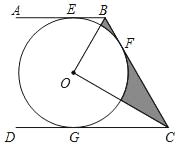
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=2cm,CO=2![]() cm.
cm.
(1)求BC的长;
(2)求图中阴影部分的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)AB、BC、CD分别与○O相切于E,F,G,分析可得∠OBF=![]() ∠EBF,∠OCF=
∠EBF,∠OCF=![]() ∠GCF;再由AB∥CD可得∠BOC=90°,故可求出BC的长
∠GCF;再由AB∥CD可得∠BOC=90°,故可求出BC的长
(2)连接OF,用等积法求出OF的长,即可求出△BOC内的扇形面积,再求出△BOC的面积,用△BOC的面积减去△BOC内的扇形面积即可求出阴影面积
解:(1)∵ AB、BC、CD分别与○O相切于E,F,G
∴∠OBF=![]() ∠EBF,∠OCF=
∠EBF,∠OCF=![]() ∠GCF
∠GCF
∵AB∥CD ∴∠EBF+∠GCF=180°
∴∠OBF+∠OCF==![]() ∠EBF+
∠EBF+![]() ∠GCF=90°
∠GCF=90°
∴∠ BOC=90°
BC=![]() =
=![]() =4
=4
(2)连接OF,∵ BC与○O相切于F∴OF⊥BC
又∵![]() BO
BO![]() CO=
CO=![]() BC
BC![]() OF
OF
∴![]()
∴OF=![]()
∴![]() =2
=2![]()



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )

A.第24天的销售量为300件
B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元
D.第15天与第30天的日销售量相等
查看答案和解析>>
科目:初中数学 来源: 题型:
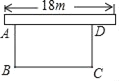
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正如我们小学学过的圆锥体积公式 ![]() (
(![]() 表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到
表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到![]() .祖冲之是世界上第一个把
.祖冲之是世界上第一个把![]() 计算到小数点后第7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把
计算到小数点后第7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把![]() 计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内,即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习。下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于
计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内,即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习。下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于 ![]() ,则这个圆锥的高等于().
,则这个圆锥的高等于().
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
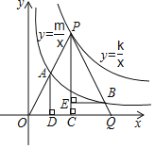
【题目】如图,在第一象限内,动点P在反比例函数y=![]() 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=
的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=![]() 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
①![]() 为定值;②若k=4m,则A为OP中点;③S△PEB=
为定值;②若k=4m,则A为OP中点;③S△PEB=![]() ;④OA2+PB2=PQ2.
;④OA2+PB2=PQ2.
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com