
【题目】为践行“绿水青山就是金山银山”的理念,及时推广生态文明建设,某校组织全校师生参与植树节活动.为调査栽种的柳树的成活情况,对全校学生的植树情况进行了抽样调查,并将调查结果分为“A.优良”“B.合格”C.差”三类.
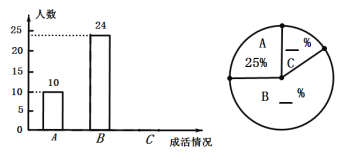
请根据图中信息,解答下列问题.
(1)求被调查学生的人数.
(2)将上面的条形统计图与扇形统计图补充完整.
(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人),A类1棵,B类2棵,C类1棵,该小组恰好有两棵树被抽査,求恰好是两棵B类树被抽查的概率.
【答案】(1)40(2)见解析(3)![]()
【解析】
(1)由A类人数及其所占百分比可得总人数;
(2)总人数减去A、B的人数求得C类人数,再分别用B、C的人数除以总人数可得对应百分比,据此即可补全图形;
(3)列表得出所有等可能结果,再根据概率公式求解可得.
(1)全班学生总人数为10÷25%=40(人);
(2)∵C类人数为40-(10+24)=6,
∴C类所占百分比为![]() ×100%=15%,B类百分比为
×100%=15%,B类百分比为![]() ×100%=60%,
×100%=60%,
补全图形如下:
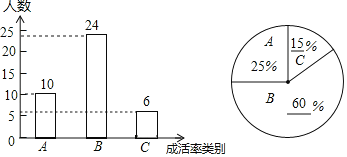
(3)列表如下:
A | B | B | C | |
A | BA | BA | CA | |
B | AB | BB | CB | |
B | AB | BB | CB | |
C | AC | BC | BC |
由表可知,共有12种等可能结果,其中全是B类的有2种情况,
所以全是B类学生的概率为![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
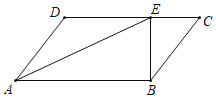
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是某地区今年4月份的囗平均气温的频数分布直方图(直方图中每一组数都包括前一个边界值,不包括后一个边界值),则下列结论中错误的是( )
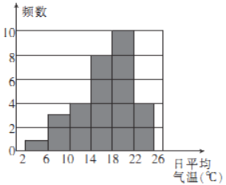
A.该地区4月份的口平均气温在18℃以上(含18℃)的共有10天
B.该直方图的组距是4℃
C.该地区4月份的口平均气温的最大值至少是22℃
D.该直方图中口平均气温为6~10℃的这一组数的频数为3,频率为0.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=20,DA⊥AB,E是⊙O上一点,连接DE并延长交AB的延长线于点F,DE=DA,BF=16.
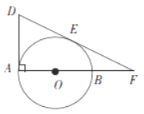
(1)求证:DE是⊙O的切线.
(2)求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .
.

(Ⅰ)如图Ⅰ,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.
(Ⅱ)如图Ⅱ,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 的结论是否仍然成立?并请你说明理由;
的结论是否仍然成立?并请你说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°.
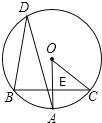
(1)求∠AOC的度数.
(2)若弦BC=8cm,求图中劣弧BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6![]() ,BC=3
,BC=3![]() 动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
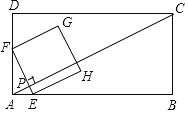
(1)①AC= .②当点F在AD上时,用含t的代数式直接表示线段PF的长 .
(2)当点F与点D重合时,求t的值.
(3)设方形EFGH的周长为l,求l与t之间的函数关系式.
(4)直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com