
【题目】在![]() 中,
中,![]() ,
,![]() .
.

(Ⅰ)如图Ⅰ,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.
(Ⅱ)如图Ⅱ,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 的结论是否仍然成立?并请你说明理由;
的结论是否仍然成立?并请你说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
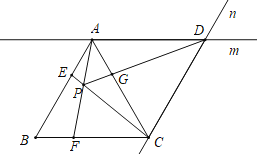
【题目】如图,在等边△ABC中,点E,F分别是边AB,BC上的动点(不与端点重合),且始终保持AE=BF,连接AF,CE相交于点P过点A作直线m∥BC,过点C作直线n∥AB,直线m,n相交于点D,连接PD交AC于点G,在点E,F的运动过程中,若![]() =
=![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
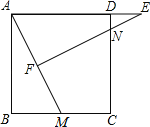
【题目】如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:![]() .
.
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,及时推广生态文明建设,某校组织全校师生参与植树节活动.为调査栽种的柳树的成活情况,对全校学生的植树情况进行了抽样调查,并将调查结果分为“A.优良”“B.合格”C.差”三类.
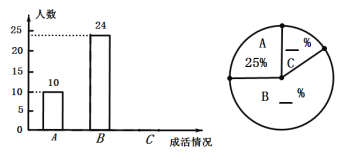
请根据图中信息,解答下列问题.
(1)求被调查学生的人数.
(2)将上面的条形统计图与扇形统计图补充完整.
(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人),A类1棵,B类2棵,C类1棵,该小组恰好有两棵树被抽査,求恰好是两棵B类树被抽查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数).
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点;
(2)设抛物线的顶点为A,与x轴两个交点分别为B,D,B在D的右侧,与y轴的交点为C.
①求证:当m取不同值时,△ABD都是等边三角形;
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2.

(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= ,OC△OA= ;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
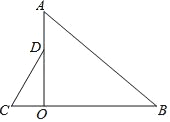
【题目】如图,△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在OA上.将△COD绕点O顺时针旋转一周,在旋转过程中,当旋转角是_____°时,CD∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
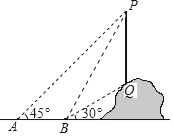
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com