
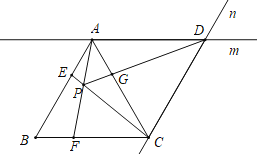
【题目】如图,在等边△ABC中,点E,F分别是边AB,BC上的动点(不与端点重合),且始终保持AE=BF,连接AF,CE相交于点P过点A作直线m∥BC,过点C作直线n∥AB,直线m,n相交于点D,连接PD交AC于点G,在点E,F的运动过程中,若![]() =
=![]() ,则
,则![]() 的值为_____.
的值为_____.
【答案】![]() ,
,![]()
【解析】
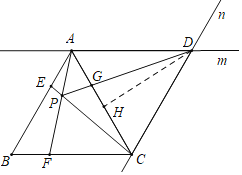
作DH⊥AC于H,由“SAS”可证△ABF≌△CAE,可得∠BAF=∠ACE,可求∠CPF=60°,通过证明A,P,C,D四点共圆,可得∠ACP=∠ADP,∠APD=∠ACD=60°,通过证明△DAG∽△DPA,可得DA2=DGDP=20k2,可求DA的长,由勾股定理可求GH的长,即可求解.
解:作DH⊥AC于H,
∵△ABC是等边三角形,
∴AC=AB,∠B=∠CAE=60°,且AE=BF,
∴△ABF≌△CAE(SAS),
∴∠BAF=∠ACE,
∴∠CPF=∠ACP+∠CAP=∠BAF+∠CAP=∠CAB=60°,
∵m∥BC,n∥AB,
∴∠DAC=∠ACB=60°,∠ACD=∠BAC=60°,
∴△ADC是等边三角形,
∴∠ADC=60°,
∵∠APC+∠ADC=180°,
∴A,P,C,D四点共圆,
∴∠ACP=∠ADP,∠APD=∠ACD=60°
∵![]()
∴可以假设PG=k,DG=4k,
∵∠ADG=∠ADP,∠DAG=∠DPA=60°,
∴△DAG∽△DPA,
∴DA2=DGDP=20k2,
∵DA>0
∴![]()
∴![]()
在Rt△DGH中,![]()
∴![]()
∴![]()
当点G在点H下方时,根据对称性可得:![]()
故答案为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
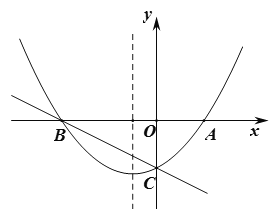
【题目】如图,对称轴是![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 若点
若点![]() 是直线
是直线![]() 下方的抛物线上的动点,求
下方的抛物线上的动点,求![]() 的面积的最大值;
的面积的最大值;
![]() 若点
若点![]() 在抛物线对称轴左侧的抛物线上运动,过点
在抛物线对称轴左侧的抛物线上运动,过点![]() 作
作![]() 铀于点
铀于点![]() ,交直线
,交直线![]() 于点
于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在对称轴上是否存在一点
在对称轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,请求出
的周长最小,若存在,请求出![]() 点的坐标和
点的坐标和![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
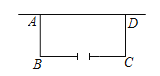
【题目】某校在基地参加社会活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留有一个宽为3米的出入口,如图所示.如何设计才能使园地的面积![]() 最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
(1)设![]() 米(
米(![]() ).
).
①![]() 米(用含
米(用含![]() 的代数式表示);
的代数式表示);
②![]() 的取值范围是 ;
的取值范围是 ;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
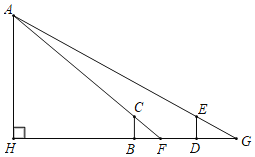
【题目】刘徽,公元3世纪人,是中国历史上最杰出的数学家之一.《九章算术注》和《海岛算经》是他留给后世最宝贵的数学遗产.《海岛算经》第一个问题的大意是:如图,要测量海岛上一座山峰A的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从DE退行127步到点G处,从G观察A点,A,E,G三点也成一线,试计算山峰的高度AH及BH的长(这里古制1步=6尺,1里=180丈=1800尺=300步,结果用步来表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
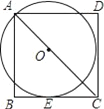
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的
⊙ O与BC相切于点E.
(1)求证:CD是⊙ O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .
.

(Ⅰ)如图Ⅰ,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.
(Ⅱ)如图Ⅱ,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 的结论是否仍然成立?并请你说明理由;
的结论是否仍然成立?并请你说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com