
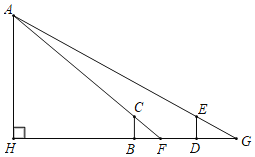
【题目】刘徽,公元3世纪人,是中国历史上最杰出的数学家之一.《九章算术注》和《海岛算经》是他留给后世最宝贵的数学遗产.《海岛算经》第一个问题的大意是:如图,要测量海岛上一座山峰A的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从DE退行127步到点G处,从G观察A点,A,E,G三点也成一线,试计算山峰的高度AH及BH的长(这里古制1步=6尺,1里=180丈=1800尺=300步,结果用步来表示).
科目:初中数学 来源: 题型:
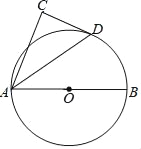
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件20元购进一批衬衫,若以每件40元出售,则每天可售出60件,经调查发现,如果每件衬衫每涨价1元,商场平均每天可少售出2件,若设每件衬衫涨价![]() 元,回答下列问题:
元,回答下列问题:
(1)该商场每天售出衬衫 件(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 的值为多少时,商场平均每天获利1050元?
的值为多少时,商场平均每天获利1050元?
(3)该商场平均每天获利 (填“能”或“不能”)达到1250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
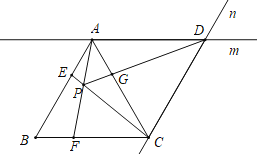
【题目】如图,在等边△ABC中,点E,F分别是边AB,BC上的动点(不与端点重合),且始终保持AE=BF,连接AF,CE相交于点P过点A作直线m∥BC,过点C作直线n∥AB,直线m,n相交于点D,连接PD交AC于点G,在点E,F的运动过程中,若![]() =
=![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
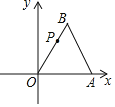
【题目】如图,以边长为4![]() +4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
+4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB表达式为y=﹣2x+2,交x轴于点A,交y轴于点B.若y轴负半轴上有一点C,且CO=![]() AO.
AO.
(1)求点C的坐标和直线AC的表达式;
(2)在直线AC上是否存在点D,使以点A、B、D为顶点的三角形与△ABO相似?若存在,请求出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com