
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析(2)6
【解析】解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC。
∴∠C+∠B=1800,∠ADF=∠DEC。
∵∠AFD+∠AFE=1800,∠AFE=∠B,∴∠AFD=∠C。
在△ADF与△DEC中,∵∠AFD=∠C,∠ADF=∠DEC,
∴△ADF∽△DEC。
(2)∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,∴
,∴![]() 。
。
在Rt△ADE中,由勾股定理得:![]() 。
。
(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC。
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在在Rt△ADE中,利用勾股定理求出线段AE的长度。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t
(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了30分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有320米
其中正确的结论有( )
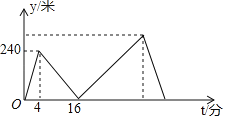
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B
,B![]() ,且满足
,且满足![]()
(1)求A、B两点的坐标;
(2)点C![]() 在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
(3)平移直线AB,交x轴正半轴于E,交y轴于F,P为直线EF上第三象限内的点,过P作PG⊥x轴于G,若S△PAB=20,且GE=12,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如图所示(部分信息未给出):
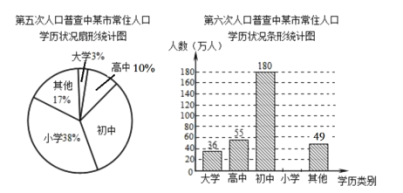
解答下列问题:
(1)求第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)求第五次人口普查中该市常住人口每万人中具有初中学历的人数;
(3)第六次人口普查结果与第五次相比,每万人中初中学历的人数增加了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题发现:如图
问题发现:如图![]() ,直线
,直线![]() ,E是AB与AD之间的一点,连接BE,CE,可以发现
,E是AB与AD之间的一点,连接BE,CE,可以发现![]() .
.
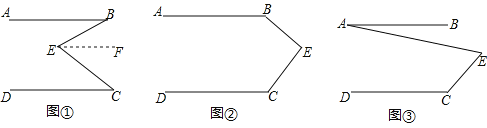
请把下面的证明过程补充完整:
证明:过点E作![]() ,
,
![]() 已知
已知![]() ,
,![]() 辅助线的作法
辅助线的作法![]() .
.
![]() ______
______![]()
![]() ______
______![]()
![]() ,
,![]() 同理
同理![]() .
.
![]() ______
______![]() 等量代换
等量代换![]()
即![]() .
.
![]() 拓展探究:如果点E运动到图
拓展探究:如果点E运动到图![]() 所示的位置,其他条件不变,进一步探究发现:
所示的位置,其他条件不变,进一步探究发现:![]() ,请说明理由.
,请说明理由.
![]() 解决问题:如图
解决问题:如图![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() ,
,![]() 分别是边长为
分别是边长为![]() 的等边
的等边![]() 边
边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() ,点
,点![]() 从顶点
从顶点![]() 同时出发,且它们的速度都为
同时出发,且它们的速度都为![]()
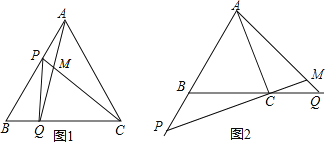
(1)连接![]() ,
,![]() 交于点
交于点![]() ,则在
,则在![]() ,
,![]() 运动的过程中,
运动的过程中,![]() 变化吗?若变化,则说明理由,若不变,则求出它的度数;
变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时![]() 是直角三角形?
是直角三角形?
(3)如图2,若点![]() ,
,![]() 在运动到终点后继续在射线
在运动到终点后继续在射线![]() ,
,![]() 上运动,直线
上运动,直线![]() ,
,![]() 交点为
交点为![]() .则
.则![]() 变化吗?若变化。则说明理由, 若不变,则求出它的度数.
变化吗?若变化。则说明理由, 若不变,则求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 的顶点
的顶点![]() 、
、![]() 处各有一只蜗牛,他们同时出发,以相同的速度分别由
处各有一只蜗牛,他们同时出发,以相同的速度分别由![]() 向
向![]() ,由
,由![]() 向
向![]() 爬行,经过
爬行,经过![]() 分钟后,它们分别爬行到了
分钟后,它们分别爬行到了![]() 、
、![]() 处,设在爬行过程中
处,设在爬行过程中![]() 与
与![]() 的交点为
的交点为![]() .
.

(1)当点![]() 、
、![]() 不是
不是![]() 、
、![]() 的中点时,图中由全等三角形吗?如果没有,请说明理由;如过有,请找出所有全等三角形,并选择其中一对进行证明
的中点时,图中由全等三角形吗?如果没有,请说明理由;如过有,请找出所有全等三角形,并选择其中一对进行证明
(2)问蜗牛在爬行过程中![]() 与
与![]() 所成的大小有无变化?请证明你的结论(提示:等边三角形的三个 都相等,每个角等于
所成的大小有无变化?请证明你的结论(提示:等边三角形的三个 都相等,每个角等于![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com