
【题目】如图,在O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°.
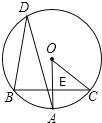
(1)求∠AOC的度数.
(2)若弦BC=8cm,求图中劣弧BC的长.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
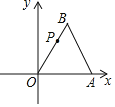
【题目】如图,以边长为4![]() +4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
+4的等边三角形AOB的顶点O为坐标原点,边OA所在直线为x轴建立平面直角坐标系,点B在第一象限,在边OB上有一点P为OB的黄金分割点(PO>PB),那么点P的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的理念,及时推广生态文明建设,某校组织全校师生参与植树节活动.为调査栽种的柳树的成活情况,对全校学生的植树情况进行了抽样调查,并将调查结果分为“A.优良”“B.合格”C.差”三类.
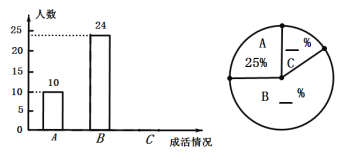
请根据图中信息,解答下列问题.
(1)求被调查学生的人数.
(2)将上面的条形统计图与扇形统计图补充完整.
(3)已知植树小组“勤奋组”的4名学生所种的四棵树中(每棵树对应一名责任人),A类1棵,B类2棵,C类1棵,该小组恰好有两棵树被抽査,求恰好是两棵B类树被抽查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2.

(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= ,OC△OA= ;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正确的结论有:

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
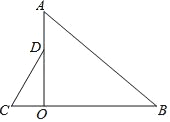
【题目】如图,△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在OA上.将△COD绕点O顺时针旋转一周,在旋转过程中,当旋转角是_____°时,CD∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
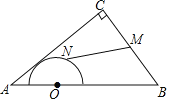
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,AD是∠BAC的角平分线.
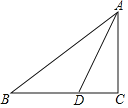
(1)请尺规作图:作⊙O,使圆心O在AB上,且AD为⊙O的一条弦.(不写作法,保留作图痕迹);
(2)判断直线BC与所作⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com