
ШчЭМ 1ЃЌЕу O ЮЊжБЯп AB ЩЯвЛЕуЃЌЙ§Еу O зїЩфЯп OCЃЌЪЙ¡ÏAOCЃК¡ÏBOC=2ЃК1ЃЌНЋжБНЧШ§НЧАх ЕФжБНЧЖЅЕуЗХдкЕу O ДІЃЌвЛБп ON дкЩфЯп OA ЩЯЃЌСэвЛБп OM дкжБЯп AB ЕФЯТЗНЃЎ
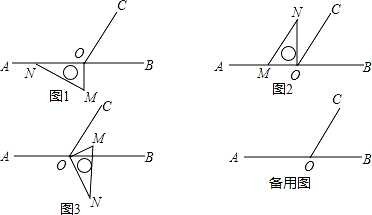
ЃЈ1ЃЉдкЭМ 1 жаЃЌ¡ÏAOC= ЃЌ¡ÏBOC= ЃЎ
НЋЭМ 1 жаЕФШ§НЧАхАДЭМ 2 ЕФЮЛжУЗХжУЃЌЪЙЕУ OM дкЩфЯп OA ЩЯЃЌдђ¡ÏCON= ЃЛ
ЃЈ3ЃЉНЋЩЯЪіжБНЧШ§НЧАхАДЭМ 3 ЕФЮЛжУЗХжУЃЌЪЙЕУ OM дк¡ÏBOC ЕФФкВПЃЌЧѓ¡ÏBONЉ¡ÏCOM ЕФЖШЪ§ЃЎ
ЁОПМЕуЁПНЧЕФМЦЫуЃЎ
ЁОзЈЬтЁПЬНОПаЭЃЎ
ЁОЗжЮіЁПЃЈ1ЃЉЕу O ЮЊжБЯп AB ЩЯвЛЕуЃЌЙ§Еу O зїЩфЯп OCЃЌЪЙ¡ÏAOCЃК¡ÏBOC=2ЃК1ЃЌПЩвдЧѓЕУ¡ÏAOC
КЭ¡ÏBOC ЕФЖШЪ§ЃЛ
ИљОн¡ÏAOC ЕФЖШЪ§КЭ¡ÏMON ЕФЖШЪ§ПЩвдЕУЕН¡ÏCON ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИљОн¡ÏBOC=60ЁуЃЌ¡ÏMON=90ЁуЃЌ¡ÏBON=¡ÏMONЉ¡ÏBOMЃЌ¡ÏCOM=¡ÏBOCЉ¡ÏBOMЃЌПЩвд ЕУЕН¡ÏBONЉ¡ÏCOM ЕФЖШЪ§ЃЎ
ЁОНтД№ЁПНтЃКЃЈ1ЃЉ¡ßЕу O ЮЊжБЯп AB ЩЯвЛЕуЃЌЙ§Еу O зїЩфЯп OCЃЌЪЙ¡ÏAOCЃК¡ÏBOC=2ЃК1ЃЌ
¡ÏAOC+¡ÏBOC=180ЁуЃЌ
¡ЈЄ¡ÏAOC=120ЁуЃЌ¡ÏBOC=60Ёу
ЙЪД№АИЮЊЃК120ЁуЃЌ60ЁуЃЛ
¡ßгЩЃЈ1ЃЉПЩжЊЃК¡ÏAOC=120ЁуЃЌ¡ÏMON=90ЁуЃЌ¡ÏAOC=¡ÏMON+¡ÏCONЃЌ
¡ЈЄ¡ÏCON=¡ÏAOCЉ¡ÏMON=120ЁуЉ90Ёу=30ЁуЃЌ
ЙЪД№АИЮЊЃК30ЁуЃЛ
ЃЈ3ЃЉгЩЭМПЩжЊЃК¡ÏBOC=60ЁуЃЌ¡ÏMON=90ЁуЃЌ¡ÏBON=¡ÏMONЉ¡ÏBOMЃЌ¡ÏCOM=¡ÏBOCЉ¡ÏBOMЃЌ дђЃЌ¡ÏBONЉ¡ÏCOM=90ЁуЉ¡ÏBOMЉЃЈ60ЁуЉ¡ÏBOMЃЉ=30ЁуЃЌ
МД¡ÏBONЉ¡ÏCOM ЕФЖШЪ§ЪЧ 30ЁуЃЎ
ЁОЕуЦРЁПБОЬтПМВщНЧЕФМЦЫуЃЌНтЬтЕФЙиМќЪЧевГіИїИіНЧжЎМфЕФЙиЯЕЃЌгывбжЊЬѕМўНЈСЂЙиЯЕЃЌШЛКѓЧѓ ГіЫљ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ФГбЇаЃ 2015ЁЋ2016 бЇФъЖШЦпФъМЖШ§Арга 50 УћбЇЩњЃЌЯжЖдбЇЩњзюЯВЛЖЕФЧђРрдЫЖЏНјааСЫЕїВщЃЌ ИљОнЕїВщЕФНсЙћжЦзїСЫЩШаЮЭГМЦЭМЃЌШчЭМЫљЪОЃЎИљОнЩШаЮЭГМЦЭМжаЬсЙЉЕФаХЯЂЃЌИјГівдЯТНсТлЃК
?зюЯВЛЖзуЧђЕФШЫЪ§зюЖрЃЌДяЕНСЫ 15 ШЫЃЛ
?зюЯВЛЖг№УЋЧђЕФШЫЪ§зюЩйЃЌжЛга 5 ШЫЃЛ
?зюЯВЛЖХХЧђЕФШЫЪ§БШзюЯВЛЖЦЙХвЧђЕФШЫЪ§Щй 3 ШЫЃЛ
?зюЯВЛЖЦЙХвЧђЕФШЫЪ§БШзюЯВЛЖРКЧђЕФШЫЪ§Жр 6 ШЫЃЎ Цфжае§ШЗЕФНсТлгаЃЈ ЃЉ
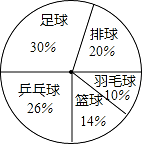
AЃЎ1 Иі BЃЎ2 Иі CЃЎ3 Иі DЃЎ4 Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШчЭМвбжЊЕу C ЮЊ AB ЩЯвЛЕуЃЌAC=12cmЃЌCB= ACЃЌDЁЂE ЗжБ№ЮЊ ACЁЂAB ЕФжаЕуЃЌЧѓ DE ЕФ ГЄЃЎ
ACЃЌDЁЂE ЗжБ№ЮЊ ACЁЂAB ЕФжаЕуЃЌЧѓ DE ЕФ ГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
Шє x+m гы x+3 ЕФГЫЛ§жаВЛКЌ x ЕФвЛДЮЯюЃЌдђ m ЕФжЕЮЊЃЈ ЃЉ
AЃЎ0 BЃЎ1 CЃЎ3 DЃЎЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
дкЯТСаЖўДЮИљЪНжаЃЌгы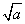 ЪЧЭЌРрЖўДЮИљЪНЕФЪЧЁЁЁЁЁЃЈ ЃЉ
ЪЧЭЌРрЖўДЮИљЪНЕФЪЧЁЁЁЁЁЃЈ ЃЉ
ЃЈAЃЉ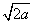 ЃЈBЃЉ
ЃЈBЃЉ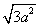 ЃЈCЃЉ
ЃЈCЃЉ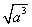 ЃЈDЃЉ
ЃЈDЃЉ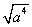
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШчЭМЃЌе§ЗНаЮOABCЃЌADEFЕФЖЅЕуAЁЂDЁЂCдкзјБъжсЩЯЃЌЕуFдкAB ЩЯЃЌЕуBЁЂEдкКЏЪ§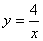 ЃЈ
ЃЈ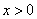 ЃЉЕФЭМЯѓЩЯЃЌШєвѕгАВПЗжЕФУцЛ§ЮЊ12 -
ЃЉЕФЭМЯѓЩЯЃЌШєвѕгАВПЗжЕФУцЛ§ЮЊ12 -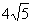 ЃЌдђЕуEЕФзјБъЪЧ .
ЃЌдђЕуEЕФзјБъЪЧ .

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com