
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② ![]() ;③ac-b+1=0;④OA·OB=
;③ac-b+1=0;④OA·OB= ![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )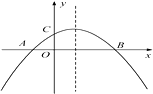
A.4
B.3
C.2
D.1
【答案】B
【解析】观察函数图象,发现:
开口向下a<0;与y轴交点在y轴正半轴c>0;对称轴在y轴右侧﹣ ![]() >0;顶点在x轴上方
>0;顶点在x轴上方 ![]() >0.
>0.
①∵a<0,c>0,﹣ ![]() >0,
>0,
∴b>0,
∴abc<0,①成立;
②∵ ![]() >0,
>0,
∴ ![]() <0,②不成立;
<0,②不成立;
③∵OA=OC,
∴xA=﹣c,
将点A(﹣c,0)代入y=ax2+bx+c中,
得:ac2﹣bc+c=0,即ac﹣b+1=0,③成立;
④∵OA=﹣xA,OB=xB,xAxB= ![]() ,
,
∴OAOB=﹣ ![]() ,④成立.
,④成立.
综上可知:①③④成立.
故答案为:①③④.
观察函数图像,由抛物线开口方向得a<0,由抛物线的对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,则可对①进行判断;根据抛物线与x轴的交点个数得到b2-4ac>0,加上a<0,则可对②进行判断;利用OA=OC可得到A(-c,0),再把A(-c,0)代入y=ax2+bx+c得ac2-bc+c=0,两边除以c则可对③进行判断;设A(x1,0),B(x2,0),则OA=-x1,OB=x2,根据抛物线与x轴的交点问题得到x1和x2是方程ax2+bx+c=0(a≠0)的两根,利用根与系数的关系即可对④进行判断,从而得出答案。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,两直线l1:y=kx﹣2b+1和l2:y=(1﹣k)x+b﹣1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2.
(1)求这两条直线的解析式;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的
的![]() 边的异侧作
边的异侧作![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
(1)如图,若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,试解决下面两个问题:
,试解决下面两个问题:
①如图2,![]() ,求
,求![]() 的度数;
的度数;
②如图3,若![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
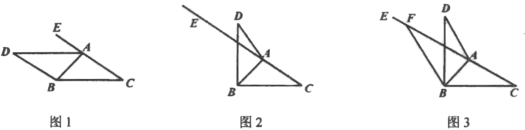
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
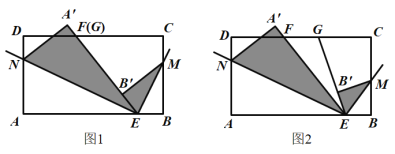
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com