
【题目】如图,两直线l1:y=kx﹣2b+1和l2:y=(1﹣k)x+b﹣1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2.
(1)求这两条直线的解析式;
(2)求△ABC的面积.

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】为选拔参加八年级数学“拓展性课程”活动人选,数学李老师对本班甲、乙两名学生以前经历的10次测验成绩(分)进行了整理、分析(见图①):

(1)写出a,b的值;
(2)如要推选1名学生参加,你推荐谁?请说明你推荐的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩![]() 满分为10分
满分为10分![]() 统计如下:
统计如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,10
,10
![]() 分及以上为A级,
分及以上为A级,![]() 分为B级
分为B级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分为C级
分为C级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分以下为D级
分以下为D级![]() 请把下面表格补充完整;
请把下面表格补充完整;
等级 | A | B | C | D |
人数 | 4 | 8 |
![]() 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少;
![]() 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于二次三项式 ![]() ,能直接用公式法进行因式分解,得到
,能直接用公式法进行因式分解,得到 ![]() ,但对于二次三项式
,但对于二次三项式 ![]() ,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式
,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式 ![]() 中先加上一项
中先加上一项 ![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 ![]() 这项,使整个式子的值不变,于是:
这项,使整个式子的值不变,于是:

像这样把二次三项式分解因式的方法叫做添(拆)项法.
![]() 问题解决:请用上述方法将二次三项式
问题解决:请用上述方法将二次三项式 ![]() 分解因式.
分解因式.
(2)拓展应用:二次三项式 ![]() 有最小值或有最大值吗?如果有,请你求出来并说明理由.
有最小值或有最大值吗?如果有,请你求出来并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点都在网格的格点上.
(1)把△ABC向下平移6个单位长度,再向左平移5个单位长度,得到△A1B1C1.请直接写出点A1、点B1和点C1的坐标.(不需要画图)
(2)求△ABC的面积.
(3)点D的坐标为(-3,1),在坐标轴上是否存在点E使得△BDE的面积等于△ABC的面积,若存在,请直接写出点E的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.图象必经过点(-1,5)
B.图象的两个分支分布在第二、四象限
C.y随x的增大而增大
D.若x>1,则-5<y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.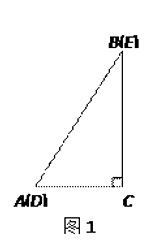
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是;
②设△BDC的面积为S1 , △AEC的面积为S2 , 则S1与S2的数量关系是.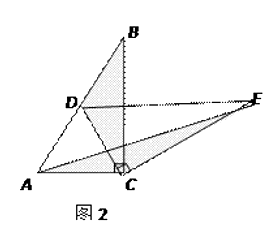
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.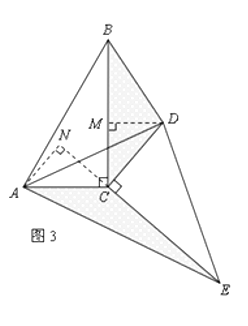
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使 ![]() ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② ![]() ;③ac-b+1=0;④OA·OB=
;③ac-b+1=0;④OA·OB= ![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )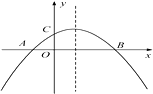
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com