
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.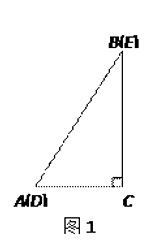
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是;
②设△BDC的面积为S1 , △AEC的面积为S2 , 则S1与S2的数量关系是.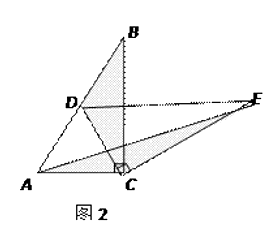
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.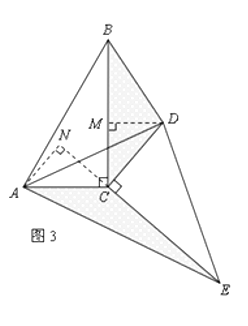
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使 ![]() ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.
【答案】
(1)DE∥AC,S1=S2
(2)解:如图,∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
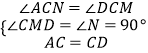 ,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2
(3)解:如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,
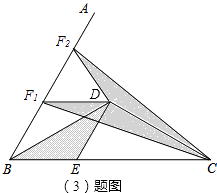
所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD= ![]() ∠ABC=30°,∠F2DB=90°,
∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB= ![]() ×60°=30°,
×60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,
∠CDF2=360°﹣150°﹣60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
 ,
,
∴△CDF1≌△CDF2(SAS),
∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,
∴∠DBC=∠BDE=∠ABD= ![]() ×60°=30°,
×60°=30°,
又∵BD=4,
∴BE= ![]() ×4÷cos30°=2÷
×4÷cos30°=2÷ ![]() =
= ![]() ,
,
∴BF1= ![]() ,BF2=BF1+F1F2=
,BF2=BF1+F1F2= ![]() +
+ ![]() =
= ![]() ,
,
故BF的长为 ![]() 或
或 ![]() .
.
【解析】解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=AC= ![]() AB,
AB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
故答案为:DE∥AC;S1=S2;
(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答.
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=![]() AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答。
AB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答。
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明.
(3)过点D作DF1∥BE,求出四边形BEDF1是菱形,根据菱形的对边相等可得BE=DF1,然后根据等底等高的三角形的面积相等可知点F1为所求的点,过点D作DF2⊥BD,求出∠F1DF2=60°,从而得到△DF1F2是等边三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“边角边”证明△CDF1和△CDF2全等,根据全等三角形的面积相等可得点F2也是所求的点,然后在等腰△BDE中求出BE的长,可得到BF1的长再根据BF2=BF1+F1F2即可得解。


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】真假命题的思考.
一天,老师在黑板上写下了下列三个命题:
①垂直于同一条直线的两条直线平行;
②若![]() ,则
,则![]()
③若![]() 和
和![]() 的两边所在直线分别平行,则
的两边所在直线分别平行,则![]() .
.
小明和小丽对话如下,
小明:“命题①是真命题,好像可以证明.”
小丽:“命题①是假命题,好像少了一些条件.”
(1)结合小明和小丽的对话,谈谈你的观点.如果你认为是真命题,请证明:如果你认为是假命题,请增加一个适当的条件,使之成真命题.
(2)请在命题②、命题③中选一个,如果你认为它是真命题,请证明:如果你认为它是假命题,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线l1:y=kx﹣2b+1和l2:y=(1﹣k)x+b﹣1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2.
(1)求这两条直线的解析式;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的AEMG的面积S1与HCFM的面积S2的大小关系是( )

A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
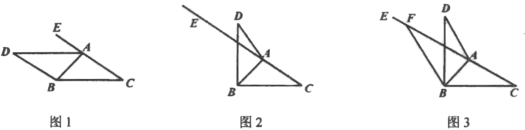
【题目】如图,在![]() 的
的![]() 边的异侧作
边的异侧作![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
(1)如图,若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,试解决下面两个问题:
,试解决下面两个问题:
①如图2,![]() ,求
,求![]() 的度数;
的度数;
②如图3,若![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com