练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在四边形中，与的角平分线交于点，，过点作交于点，，，连接，，则__________．

    【答案】4

    【解析】

    根据∠DEC的度数以及角平分线的定义算出∠A+∠ABC=230°，再结合AD∥BF，得出∠CBF=50°，利用算出∠BFC=90°，最后根据和算出结果.

    解：∵，

    ∴∠EDC+∠ECD=180°-115°=65°，

    又∵与的角平分线交于点，

    ∴∠ADC+∠BCD=65°×2=130°，

    ∴∠A+∠ABC=360°-130°=230°，

    ∵AD∥BF，

    ∴∠A+∠ABF=180°，

    ∴∠CBF=230°-180°=50°，

    ∵，

    ∴∠BCE=40°，

    ∴∠BFC=90°，

    ∵，BF＞0，

    ∴，

    解得：x=2，

    即CE=2×2=4.

    故答案为：4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明进行了以下探索：

    设（其中均为整数），则有．

    ∴．这样小明就找到了一种把部分的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    当均为正整数时，若，用含m、n的式子分别表示，得＝　 　，＝　 　；

    （2）利用所探索的结论，找一组正整数，填空： ＋　 　＝(　 　＋　 　)2；

    （3）若，且均为正整数，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，有四个点A（﹣8，3）、B（﹣4，5）、C（0，n）、D（m，0），当四边形ABCD的周长最短时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数 ，则下列结论不正确的是( )
    A.图象必经过点（-1，5）
    B.图象的两个分支分布在第二、四象限
    C.y随x的增大而增大
    D.若x＞1，则－5＜y＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面说法正确的个数有（ ）

    （1）二元一次方程组的两个方程的所有解，叫做二元一次方程组的解；

    （2）如果，则；

    （3）三角形的外角等于与它不相邻的两个内角的和；

    （4）多边形内角和等于；

    （5）一组数据1，2，3，4，5的众数是0

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.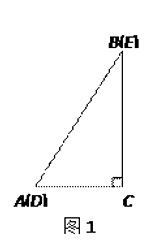

    （1）操作发现
    如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：
    ①线段DE与AC的位置关系是；
    ②设△BDC的面积为S1 ， △AEC的面积为S2 ， 则S1与S2的数量关系是.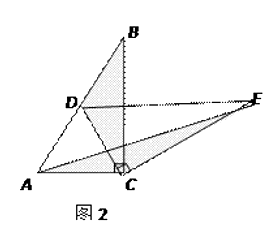

    （2）猜想论证
    当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.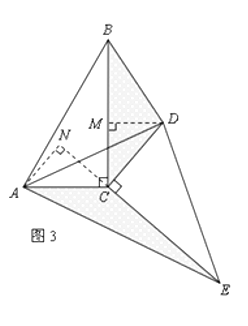

    （3）拓展探究
    已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.若在射线BA上存在点F，使 ，请直接写出相应的BF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在平面直角坐标系中，且A、B、C.将其平移后得到，若A，B的对应点是，，C的对应点的坐标是.

    （1）在平面直角坐标系中画出△ABC；

    （2）写出点的坐标是_____________,坐标是___________;

    （3）此次平移也可看作向________平移了____________个单位长度，再向_______平移了______个单位长度得到△ABC.

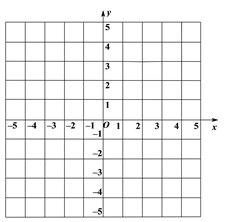
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式(整数可看作分母为1的分数)，那么无限循环小数如何表示为分数形式呢？请看以下示例：

    例：将化为分数形式，

    由于，设，①

    得，②

    ②①得,解得,于是得.

    同理可得,.

    根据以上阅读,回答下列问题：(以下计算结果均用最简分数表示)

    （类比应用）

    (1) ；

    (2)将化为分数形式，写出推导过程；

    （迁移提升）

    (3) ， ；(注,）

    （拓展发现）

    (4)若已知，则 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一批共享单车需要维修，维修后继续投放骑用，现有甲、乙两人做维修，甲每天维修16辆，乙每天维修的车辆比甲多8辆，甲单独维修完成这批共享单车比乙单独维修完多用20天，公司每天付甲80元维修费，付乙120元维修费．

    （1）问需要维修的这批共享单车共有多少辆？

    （2）在维修过程中，公司要派一名人员进行质量监督，公司负担他每天10元补助费，现有三种维修方案：①由甲单独维修；

    ②由乙单独维修；

    ③甲、乙合作同时维修，你认为哪种方案最省钱，为什么？

    查看答案和解析>>

    同步练习册答案