
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况: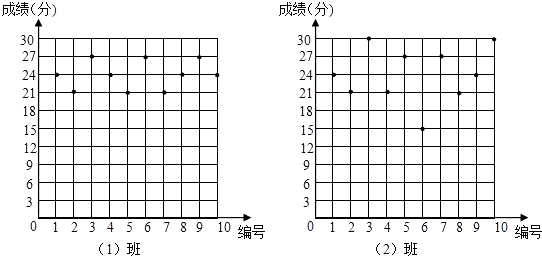
(1)利用图中提供的信息,补全下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | 24 | |
(2)班 | 24 |
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?
【答案】
(1)24,24,21
(2)解:(1)班成绩优秀人数=60× ![]() =42(名),(2)班成绩优秀人数=60×
=42(名),(2)班成绩优秀人数=60× ![]() =36(名)
=36(名)
答:(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀
(3)解:因为(1)班的极差=27﹣21=6,(2)班的极差=30﹣15=15,所以(1)班的学生纠错的整体情况更好一些
【解析】解:(1)
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | ||
(2)班 | 24 | 21 |
(2)(1)班成绩优秀人数=60× 7 10 =42(名),(2)班成绩优秀人数=60× 6 10 =36(名)
答:(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀
(3)因为(1)班的极差=27﹣21=6,(2)班的极差=30﹣15=15,所以(1)班的学生纠错的整体情况更好一些


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
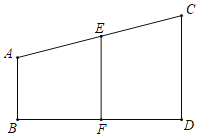
【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB= ( )
∴∠ABD+∠CDB=180°
∴AB∥ ( )
又∠A与∠AEF互补 ( )
∠A+∠AEF=
∴AB∥ ( )
∴CD∥EF ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一条腰长为 . 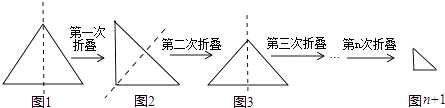
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
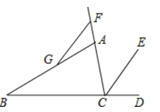
【题目】如图,CE是∠ACD的角平分线,F为CA延长线上一点,G为线段AB上一点,连接FG.
(1)若∠ACD=110°,∠AFG=55°,试说明:FG∥CE
(2)若∠AGF=20°,∠BAC=45°,且FG∥CE,求∠ACE的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
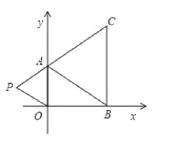
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a.b.c满足关系式![]() ,c是64的算术平方根.
,c是64的算术平方根.
(1)直接写出a,b,c的值:a=____,b=____,c= ____;
(2)如果在第二象限内有一点P(m,2),请用含m的式子表示四边形APOB的面积S![]() ;
;
(3)在(2)的条件下,是否存在点P,使四边形APOB的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
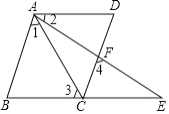
【题目】填空:已知:如图,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:∵![]()
∴________(内错角相等,两直线平行)
∴![]() ________(两直线平行,内错角相等)
________(两直线平行,内错角相等)
∵![]()
∴![]() (________________)
(________________)
∵![]()
∴![]() ,(________________)
,(________________)
即![]() ________
________
∴![]()
∴![]() (同位角相等,两直线平行).
(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com