
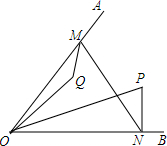
 如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$.
如图,∠AOB=60°,∠POQ=30°,OQ=2,OP=3,点M、N分别在OA、OB上,则PN+MN+QM的最小值为$\sqrt{13}$. 分析 作点P关于直线OB的对称点P′,作点Q关于直线OA的对称点Q′,连接P′Q′分别交OA,OB于点M、N,则点M,N即为所求,然后由轴对称的性质得:OQ′=OQ=2,OP=OP′=3,∠Q′OM=∠QOM,∠P′ON=∠PON,求得∠Q′OP′=90°,根据勾股定理即可得到结论.
解答 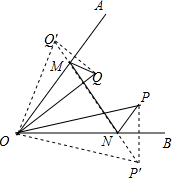 解:作点P关于直线OB的对称点P′,作点Q关于直线OA的对称点Q′,连接P′Q′分别交OA,OB于点M、N,
解:作点P关于直线OB的对称点P′,作点Q关于直线OA的对称点Q′,连接P′Q′分别交OA,OB于点M、N,
则线段P′Q′的长度就是PN+MN+QM的最小值,
由轴对称的性质得:OQ′=OQ=2,OP=OP′=3,
∠Q′OM=∠QOM,∠P′ON=∠PON,
∵∠AOB=60°,∠POQ=30°,
∴∠MOQ+∠P′ON=30°,
∴∠Q′OM+∠P′ON=30°,
∴∠Q′OP′=90°,
∴Q′P′=$\sqrt{OQ{′}^{2}+OP{′}^{2}}$=$\sqrt{13}$,
∴PN+MN+QM的最小值为$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
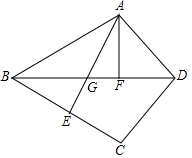 已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.如图,求证:∠EAF=∠ABD.
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.如图,求证:∠EAF=∠ABD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则中间小正方形与大正方形的面积差是( )
“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则中间小正方形与大正方形的面积差是( )| A. | -9 | B. | -36 | C. | -27 | D. | -34 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
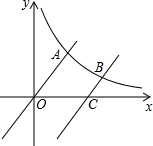 如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )
如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
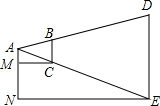 如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.
如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆.已知此同学的臂长约为60cm,求旗杆的大致高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com