
ЎҫМвДҝЎҝИзНјЈ¬ФЪ8ЎБ8өДХэ·ҪРОНшёсЦРЈ¬ГҝёцРЎХэ·ҪРОөДұЯіӨ¶јОӘ1ёцөҘО»іӨ¶ИЈ¬ЎчABCөД¶Ҙөг¶јФЪХэ·ҪРОНшёсөДёсөгЙПЈ®
ЈЁ1Ј©Ҫ«ЎчABCҫӯЖҪТЖәуөГөҪЎчAЎдBЎдCЎдЈ¬өгAөД¶ФУҰөгКЗөгAЎдЈ®»ӯіцЖҪТЖәуЛщөГөДЎчAЎдBЎдCЎдЈ»
ЈЁ2Ј©Б¬ҪУAAЎдЎўCCЎдЈ¬ФтЛДұЯРОAAЎдCЎдCөДГж»эОӘЎЎ________Ј®
ЈЁ3Ј©ИфБ¬ҪУAAЎдЈ¬BBЎдЈ¬ФтХвБҪМхПЯ¶ОЦ®јдөД№ШПөКЗЎЎ ЎЎЈ»
ЈЁ4Ј©ЎчABCөДёЯCDЛщФЪЦұПЯұШҫӯ№эНјЦРөДТ»ёцёсөгөгPЈ¬ФЪНјЦРұкіцөгPЈ®

Ўҫҙр°ёЎҝЈЁ1Ј©јыҪвОцЈ»ЈЁ2Ј©6Ј»ЈЁ3Ј©ЖҪРРЗТПаөИЈ»ЈЁ4Ј©јыҪвОц
ЎҫҪвОцЎҝ
ЈЁ1Ј©ЦұҪУАыУГЖҪТЖөДРФЦКөГіц¶ФУҰөгО»ЦГҪш¶шөГіцҙр°ёЈ»
ЈЁ2Ј©AAЎдЖҪРРЗТөИУЪCCЎдЈ¬AAЎдCЎдCКЗЖҪРРЛДұЯРОЈ¬ЦұҪУАыУГёоІ№·ЁЗуГж»эјҙҝЙЈ®
ЈЁ3Ј©УЙЖҪТЖөДРФЦКҝЙөГAAЎдУлBBЎдЖҪРРЗТПаөИЈ»
ЈЁ4Ј©№эCЧчABөДҙ№ПЯјҙҝЙЈ»
ЈЁ1Ј©ИзНјЛщКҫЈә

ЈЁ2Ј©УЙЖҪТЖөДРФЦКҝЙөГЈәAAЎдЖҪРРЗТөИУЪCCЎдЈ¬AAЎдCЎдCКЗЖҪРРЛДұЯРОЈ¬
АыУГёоІ№ЗуөГ![]()
№Кҙр°ёКЗЈә6Ј»
ЈЁ3Ј©УЙЖҪТЖөДРФЦКҝЙөГЈәAAЎдУлBBЎдЖҪРРЗТПаөИЈ¬
№Кҙр°ёКЗЈәЖҪРРЗТПаөИЈ»
ЈЁ4Ј©№эCЧчABөДҙ№ПЯЈ¬PөгО»ЦГИзНјЈ»



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИэҪЗРОABCИэөгөДЧшұкОӘAЈЁ-2Ј¬1Ј©Ј¬BЈЁ1Ј¬2Ј©Ј¬CЈЁkЈ¬hЈ©
ЈЁ1Ј©ФЪЦұҪЗЧшұкПөЙП»ӯіцөгAЈ¬BЈ®
ЈЁ2Ј©ИфөгCЈЁ-2Ј¬-1Ј©КұЈ¬ЗуИэҪЗРОABCөДГж»эЈ®
ЈЁ3Ј©ИфөгCФЪyЦбЙПЈ¬өұИэҪЗРОABCөДГж»эОӘ6КұЈ¬ЗуөгCөДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ҙОәҜКэy=©Ғ ![]() x+bЈЁbОӘіЈКэЈ©өДНјПуУлxЦбҪ»УЪөгAЈЁ2Ј¬0Ј©Ј¬УлyЦбҪ»УЪөгBЈ¬Ул·ҙұИАэәҜКэy=
x+bЈЁbОӘіЈКэЈ©өДНјПуУлxЦбҪ»УЪөгAЈЁ2Ј¬0Ј©Ј¬УлyЦбҪ»УЪөгBЈ¬Ул·ҙұИАэәҜКэy= ![]() өДНјПуҪ»УЪөгCЈЁ©Ғ2Ј¬mЈ©Ј®
өДНјПуҪ»УЪөгCЈЁ©Ғ2Ј¬mЈ©Ј®
ЈЁ1Ј©ЗуөгCөДЧшұкј°·ҙұИАэәҜКэөДұнҙпКҪЈ»
ЈЁ2Ј©№эөгCөДЦұПЯУлyЦбҪ»УЪөгDЈ¬ЗТSЎчCBDЈәSЎчBOC=2Јә1Ј¬ЗуөгDөДЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪ![]() ABCЦРЈ¬DКЗABЙПөДТ»өгЈ¬ЗТADЈҪ2BDЈ¬EКЗBCөДЦРөгЈ¬CDЎўAEПаҪ»УЪөгFЈ®Иф
ABCЦРЈ¬DКЗABЙПөДТ»өгЈ¬ЗТADЈҪ2BDЈ¬EКЗBCөДЦРөгЈ¬CDЎўAEПаҪ»УЪөгFЈ®Иф![]() EFCөДГж»эОӘ1Ј¬Фт
EFCөДГж»эОӘ1Ј¬Фт![]() ABCөДГж»эОӘ_____Ј®
ABCөДГж»эОӘ_____Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘИзНјЈ¬ЎПCOD=90ЎгЈ¬ЦұПЯABУлOCҪ»УЪөгBЈ¬УлODҪ»УЪөгAЈ¬ЙдПЯOEУлЙдПЯAFҪ»УЪөгGЈ®ИфOEҪ«ЎПBOA·ЦіЙ1©U2БҪІҝ·ЦЈ¬AFЖҪ·ЦЎПBADЈ¬ЎПABO=![]() ЈЁ30Ўг<
ЈЁ30Ўг<![]() <90ЎгЈ© Ј¬ФтЎПOGAөД¶ИКэОӘЈЁУГә¬
<90ЎгЈ© Ј¬ФтЎПOGAөД¶ИКэОӘЈЁУГә¬![]() өДҙъКэКҪұнКҫ)____________________Ј®
өДҙъКэКҪұнКҫ)____________________Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝС§П°јёәОөДТ»ёцЦШТӘ·Ҫ·ЁҫНКЗТӘС§»бЧҘЧЎ»щұҫНјРОЈ¬ИГОТГЗАҙЧцТ»ҙОСРҫҝРФС§П°Ј®

ЈЁ1Ј©ИзНјўЩЛщКҫөДНјРОЈ¬ПсОТГЗіЈјыөДС§П°УГЖ·Т»ФІ№жЈ¬ОТГЗіЈ°СХвСщөДНјРОҪРЧцЎ°№жРОНјЎұЈ®ЗлДг№ЫІмЎ°№жРОНјЎұЈ¬КФМҪҫҝЎПBOCУлЎПAЎўЎПBЎўЎПCЦ®јдөД№ШПөЈ¬ІўЛөГчАнУЙЈә
ЈЁ2Ј©ИзНјўЪЈ¬ИфЎчABCЦРЈ¬BOЖҪ·ЦЎПABCЈ¬COЖҪ·ЦЎПACBЈ¬ЗТЛьГЗПаҪ»УЪөгOЈ¬КФМҪҫҝЎПBOCУлЎПAөД№ШПөЈ»
ЈЁ3Ј©ИзНјўЫЈ¬ИфЎчABCЦРЈ¬ЎПABO=![]() ЎПABCЈ¬ЎПACO=
ЎПABCЈ¬ЎПACO=![]() ЎПACBЈ¬ЗТBOЎўCOПаҪ»УЪөгOЈ¬ЗлЦұҪУРҙіцЎПBOCУлЎПAөД№ШПөКҪОӘЎЎЎЎЎЎЎЎ_Ј®
ЎПACBЈ¬ЗТBOЎўCOПаҪ»УЪөгOЈ¬ЗлЦұҪУРҙіцЎПBOCУлЎПAөД№ШПөКҪОӘЎЎЎЎЎЎЎЎ_Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЦұПЯl1өДҪвОцКҪОӘ![]() Ј¬ЦұПЯl2өДҪвОцКҪОӘ
Ј¬ЦұПЯl2өДҪвОцКҪОӘ![]() Ј¬УлxЦбЎўyЦб·ЦұрҪ»УЪөгAЎўөгBЈ¬ЦұПЯl1Улl2Ҫ»УЪөгC.
Ј¬УлxЦбЎўyЦб·ЦұрҪ»УЪөгAЎўөгBЈ¬ЦұПЯl1Улl2Ҫ»УЪөгC.
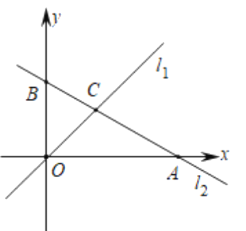

ЈЁ1Ј©ЗуөгAЎўөгBЎўөгCөДЧшұкЈ¬ІўЗуіцЎчCOBөДГж»эЈ»
ЈЁ2Ј©ИфЦұПЯl2ЙПҙжФЪөгPЈЁІ»УлBЦШәПЈ©Ј¬ВъЧгSЎчCOP=SЎчCOBЈ¬ЗлЗуіцөгPөДЧшұкЈ»
ЈЁ3Ј©ФЪyЦбУТІаУРТ»¶ҜЦұПЯЖҪРРУЪyЦбЈ¬·ЦұрУлl1Ј¬l2Ҫ»УЪөгMЎўNЈ¬ЗТөгMФЪөгNөДПВ·ҪЈ¬yЦбЙПКЗ·сҙжФЪөгQЈ¬К№ЎчMNQОӘөИСьЦұҪЗИэҪЗРОЈҝИфҙжФЪЈ¬ЗлЦұҪУРҙіцВъЧгМхјюөДөгQөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ФxЈ¬y¶ЁТеТ»ЦЦРВФЛЛгTЈ¬№ж¶ЁЈәTЈЁxЈ¬yЈ©=![]() ЈЁЖдЦРaЎўbҫщОӘ·ЗБгіЈКэЈ©Ј¬ХвАпөИКҪУТұЯКЗНЁіЈөДЛДФтФЛЛгЈ¬АэИзЈәTЈЁ0Ј¬1Ј©=
ЈЁЖдЦРaЎўbҫщОӘ·ЗБгіЈКэЈ©Ј¬ХвАпөИКҪУТұЯКЗНЁіЈөДЛДФтФЛЛгЈ¬АэИзЈәTЈЁ0Ј¬1Ј©=![]() =bЈ®
=bЈ®
ЈЁ1Ј©ТСЦӘTЈЁ2Ј¬1Ј©=![]()
ўЩЗуaЈ¬bөДЦөЈ»
ўЪИф№ШУЪmөДІ»өИКҪЧй![]() ЗЎәГУР3ёцХыКэҪвЈ¬ЗуpөДИЎЦө·¶О§Ј»
ЗЎәГУР3ёцХыКэҪвЈ¬ЗуpөДИЎЦө·¶О§Ј»
ЈЁ2Ј©ИфTЈЁxЈ¬yЈ©=TЈЁyЈ¬xЈ©¶ФИОТвУРАнКэxЈ¬y¶јіЙБўЈЁХвАпTЈЁxЈ¬yЈ©әНTЈЁyЈ¬xЈ©ҫщУРТвТеЈ©Ј¬ФтaЈ¬bУҰВъЧгФхСщөД№ШПөКҪЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҫШРОABCDөДБҪМх¶ФіЖЦбОӘЧшұкЦбЈ¬өгAөДЧшұкОӘЈЁ2,1Ј©.Т»ХЕНёГчЦҪЙП»ӯУРТ»ёцөгәНТ»МхЕЧОпПЯЈ¬ЖҪТЖНёГчЦҪЈ¬ХвёцөгУлөгAЦШәПЈ¬ҙЛКұЕЧОпПЯөДәҜКэұнҙпКҪОӘy=x2 Ј¬ ФЩҙОЖҪТЖНёГчЦҪЈ¬К№ХвёцөгУлөгCЦШәПЈ¬ФтёГЕЧОпПЯөДәҜКэұнҙпКҪұдОӘЈЁ Ј©
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com