
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图1,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2.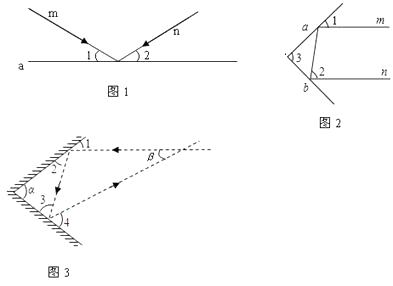
(1)如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=°,∠3=°.
(2)在(1)中m∥n,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
(4)如图3,两面镜子的夹角为α°(0<α<90)时,进入光线与离开光线的夹角为β°
(0<β<90).试探索α与β的数量关系.直接写出答案.
【答案】
(1)100;90
(2)90;90
(3)90;当∠3=90°时,m∥n.理由如下:
∵∠3=90°,
∴∠4+∠6=90°,
∴2∠4+2∠6=180°,
∴∠2+∠5=180°,
∴m∥n.
(4)![]()
【解析】解:(1)∵∠1=∠4=50°,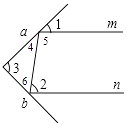
∴∠5=180°-2×50°=80°,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=100°,
∴∠6= ![]() (180°-∠2)=40°,
(180°-∠2)=40°,
∴∠3=180°-∠4-∠6=90°;
(2)同样的方法当∠1=55°,∠3=90°,∠1=40°, ∠3=90°
(3)当两平面镜a、b的夹角∠3=90°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.
(4)如图,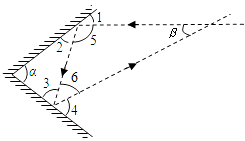
有∠5=180°-2∠2,∠6=180°-2∠3,
∵∠2+∠3=180°-∠α,
∴∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,
∴α与β的数量关系为:2α+β=180°,


科目:初中数学 来源: 题型:
【题目】为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和频率分布直方图,请你根据统计表和频率分布直方图回答下列问题: 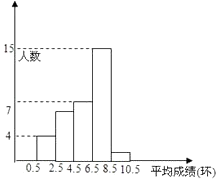
平均成绩 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数 | 0 | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
(1)参加这次射击比赛的队员有多少名?
(2)这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3)这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线nx+(n+1)y= ![]() (n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
(n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2014),则S1+S2+…+S2014的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点A(﹣2,3)向右平移a个单位长度,再向下平移b个单位长度,平移后对应的点为A′,且点A和A′关于原点对称,则a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
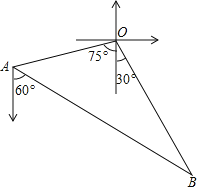
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD为平行四边形,延长AD至E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE为矩形的是( )

A. AB=BE B. BE⊥CD C. ∠ADB=900 D. CE⊥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com