
四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.

(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF-BF=EF;
(2)如图2,在(1)条件下,AG= BG,求
BG,求 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE= 。(直接写出结果)
(1)证明见解析;(2)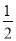 ;(3)
;(3)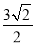 .
.
【解析】
试题分析:(1)利用△AED≌△BFA求得AE=BF,再利用线段关系求出AF-BF=EF.
(2)延长AG与DC交于点F,设BG=t先求出AB,再利用△ABG≌△FCG及直角三角形斜边上的中点,求出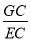 ;
;
(3)连接DG,作EM⊥BC于M点,利用直角三角形求出DG,CD的长,再利用ABG∽△DEA,求出AD,再运用△EMG∽△DEA求出EM和MG,再运用勾股定理即可求出CE的长.
试题解析:(1)∵ 四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,

∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF-BF=EF,
(2)如图2,延长AG与DC交于点F,
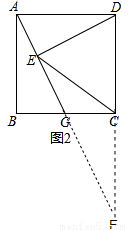
∵AG=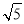 BG,设BG=t,则AG=
BG,设BG=t,则AG=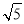 t,
t,
在Rt△ABG中,AB=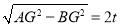 ,
,
∴G为BC的中点,
在△ABG和△FCG中,

∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴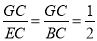 .
.
(3)如图3,连接DG,作EM⊥BC于M点,
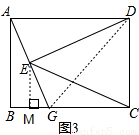
∵DE⊥AG,DE=2,GE=1,
∴在RT△DEG中,DG=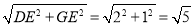 ,
,
∵CG=CD,
∴在Rt△DCG中,∠CDG=∠CGD=45°,
∴CD=CG=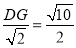 ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴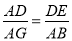 ,
,
设AD=x,则AE=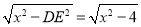 ,AG=
,AG=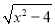 +1,
+1,
∴ ,
,
解得x1=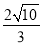 ,x2=
,x2=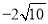 (舍去)
(舍去)
∴AE=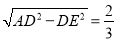 ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴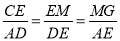 ,即
,即
解得EM= ,MG=
,MG=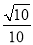 ,
,
∴CM=CG+MG=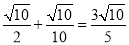 ,
,
∴CE=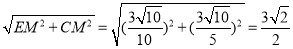 .
.
考点:四边形综合题.


科目:初中数学 来源:2015届浙江省八年级上学期第二次月考数学试卷(解析版) 题型:选择题
点P(a-1,5)和点Q(2,b-2)关于x轴对称,则 (a+b)2007的值为( )
A、0 B、-1 C、1 D、(-3)2007
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级上学期第一次月考数学试卷(解析版) 题型:选择题
下列语句是命题的是( )
A.作直线AB的垂线 B.在线段AB上取点C
C.同旁内角互补 D.垂线段最短吗?
查看答案和解析>>
科目:初中数学 来源:2015届湖北省武汉市黄陂区八年级下学期期末数学试卷(解析版) 题型:解答题
某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图.

(1)将图补充完整;
(2)本次共抽取员工50 人,每人所创年利润的众数是8万元 ,平均数是 8.12万元;
(3)若每人创造年利润10万元及(含10万元)以上位优秀员工,在公司1200员工中有多少可以评为优秀员工?
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省大连市八年级10月月考数学试卷(解析版) 题型:选择题
在△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为( )
A.50° B.75° C.100° D.125°
查看答案和解析>>
科目:初中数学 来源:2016届江苏省南京市高淳区七年级下学期期末数学试卷(解析版) 题型:选择题
在下列长度的四根木棒中,能与两根长度分别为4cm和9cm的木棒构成一个三角形的是( )
A.4cm B.5cm C.9cm D.13cm
查看答案和解析>>
科目:初中数学 来源:2015届黑龙江省绥棱县八年级五四制上学期期末考试数学试卷(解析版) 题型:选择题
等腰三角形底边长为5㎝,一腰上的中线把其周长分为两部分的差为3㎝,则腰长为( )
A.2㎝ B.8㎝ C.2㎝或8㎝ D.不确定
查看答案和解析>>
科目:初中数学 来源:2016届江苏省南京市高淳区七年级下学期期末数学试卷(解析版) 题型:选择题
若P=(x-2)(x-4),Q=(x-3)2,则P与Q的关系为( )
A.P=Q B.P>Q
C.P<Q D.P与Q的大小无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com