
【题目】如图①,点O是线段AD上一动点(不与点A、D重合),分别以AO和DO为边在AD的同侧作等边三角形OAB和等边三角形OCD,连结AC、BD相交于点E,连结OE.
(1)当点O为AD的中点时,求∠DEA的度数;
(2)在(1)的条件下,△ADE是轴对称图形吗?如果是,指出它的对称轴;如果不是,说明理由;
(3)当点O不在AD的中点时,求证EO平分∠DEA.


图① 图②
【答案】(1)∠DEA=120°(2)△ADE是轴对称图形,它的对称轴是直线OE(3)见解析
【解析】
(1)根据已知三角形OAB和三角形OCD为等边三角形,AD=OD,可知![]() ,∠BAO=60°即可求出∠BDA 的度数,同理可求出∠CAD 的度数,后可得出∠DEA的度数.
,∠BAO=60°即可求出∠BDA 的度数,同理可求出∠CAD 的度数,后可得出∠DEA的度数.
(2)根据已知条件可以证明ΔEDO≌ΔEAO,即可得出△ADE是轴对称图形,它的对称轴是直线OE .
(3)根据已知条件可证ΔAOC≌ΔBOD,结合三角形面积公式可知点O到BD,AC的距离相等,即可证得EO平分∠DEA.
(1)![]() 为等边三角形且点O为AD的中点
为等边三角形且点O为AD的中点
![]()
![]() 根据三角函数可知
根据三角函数可知![]() ,即
,即![]()
同理可求得![]()
![]() 三角形内角和为
三角形内角和为![]() ,且
,且![]() ,
,![]()
![]()
(2)![]() 为等边三角形且点O为AD的中点,
为等边三角形且点O为AD的中点, ![]() ,
,![]()
![]()
![]() 可证ΔEDO≌ΔEAO(SAS)
可证ΔEDO≌ΔEAO(SAS)
![]() 可得出△ADE是轴对称图形,它的对称轴是直线OE .
可得出△ADE是轴对称图形,它的对称轴是直线OE .
(3)![]() 为等边三角形
为等边三角形
∴可得OD=OC,OB=OA, ![]()
∴可证△AOC≌△BOD(SAS)
∴![]() ,AC=BD
,AC=BD
![]()
![]() ,AC=BD
,AC=BD
∴点O到AC、BD的距离相等(两个三角形全等,且底相等,高必然相等)
∴点O在∠DEA的角平分线上
即EO平分∠DEA


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.

(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
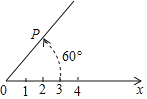
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线![]() 的解析式为y=x+1,直线
的解析式为y=x+1,直线![]() 的解析式为
的解析式为![]() ;这两个图象交于y轴上一点C,直线
;这两个图象交于y轴上一点C,直线![]() 与x轴的交点B(2,0).
与x轴的交点B(2,0).
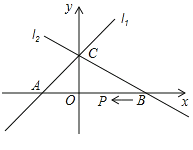
(1)求a、b的值;
(2)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′ 的坐标为 ,点B关于x轴的对称点B′ 的坐标为 ,线段AC的垂直平分线与y轴的交点D的坐标为 ;
(2)求(1)中的△A′ B′ D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形,按如图①的方式拼图,请根据图中的信息完成下列的问题

(1)在图②中用了___________块黑色正方形,在图③中用了_____________块黑色正方形;
(2)按如图的规律继续铺下去,那么第![]() 个图形要用____________块黑色正方形;
个图形要用____________块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完![]() 块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3(__________________________)
又∵HG∥CD(已知)
∴∠2=∠4(_______________________________)
∵AB∥CD(已知)
∴∠BEF+___________=180°(_____________________)
又∵EG平分∠BEF,FG平分∠EFD (已知)
∴∠1=(______)∠BEF,∠2=(______)∠EFD (______________________)
∴∠1+∠2=(________) (∠BEF +∠EFD)=(____________)
∴∠3+∠4=90°(_______________________)即∠EGF=90°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
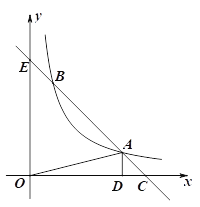
【题目】如图,已知函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交不同的点A、B,过点A作AD⊥
的图象相交不同的点A、B,过点A作AD⊥![]() 轴于点D,连接AO,其中点A的横坐标为
轴于点D,连接AO,其中点A的横坐标为![]() ,△AOD的面积为2.
,△AOD的面积为2.
(1)求![]() 的值及
的值及![]() =4时
=4时![]() 的值;
的值;
(2)记![]() 表示为不超过
表示为不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,设
,设![]() ,若
,若![]() ,求
,求![]() 值
值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com