
【题目】解不等式组
请结合题意,完成本题解答过程.
(1)解不等式①,得 ,依据是 .
(2)解不等式②,得 .
(3)解不等式③,得 .
(4)把不等式①,②和③的解集在数轴上表示出来.
(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
(6)根据不等式组的解集确立出该不等式组的最大整数解为 .
【答案】(1)x≥﹣3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变;(2)x>﹣2;(3)x<2;(4)见解析;(5)﹣2<x<2;(6)x=1.
【解析】
分别求出每一个不等式的解集,根据各不等式解集在数轴上的表示,确定不等式组的解集,并找到最大整数解.
解:(1)解不等式①,得x≥﹣3,依据是:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
(2)解不等式②,得x>﹣2.
(3)解不等式③,得x<2.
(4)把不等式①,②和③的解集在数轴上表示出来如下:

(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集:﹣2<x<2.
(6)根据不等式组的解集确立出该不等式组的最大整数解为:x=1;


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)求出y1、y2关于x的函数关系式?
(3)如果共有50人参加时,选择哪家旅行社合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE=DF,DE⊥AB,DF⊥AC,垂足分别是E、F.现有下列结论:①AD平分∠BAC;②AD⊥BC;③AD上任意一点到AB、AC的距离相等;④AD上任意一点到BC两端点的距离相等.其中正确结论的个数有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
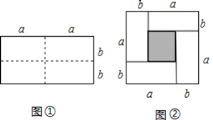
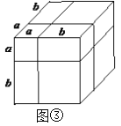
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是__________;
之间的等量关系是__________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =________;
=________;
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.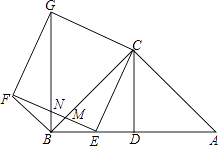
(1)证明:△CAE≌△CBG;
(2)设DE=x,BN=y,求y关于x的函数关系式,并求出y的最大值;
(3)当DE=2 ![]() ﹣2时,求∠BFE的度数.
﹣2时,求∠BFE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com