
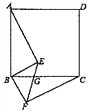
【题目】已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.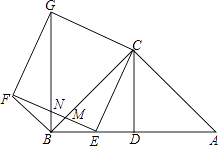
(1)证明:△CAE≌△CBG;
(2)设DE=x,BN=y,求y关于x的函数关系式,并求出y的最大值;
(3)当DE=2 ![]() ﹣2时,求∠BFE的度数.
﹣2时,求∠BFE的度数.
【答案】
(1)证明:∵四边形EFGC是正方形,
∴CG=CE,∠GCE=∠GFE=∠FEC=90°,
∵∠ACB=∠GCE=90°,
∴∠GCB=∠ECA,
∵GC=CE,CB=CA,
∴△CAE≌△CBG.
(2)解:∵CB=CA,CD⊥AB,∠ACB=90°,
∴CD=BD=AD=2,∠CBA=∠A=45°,
∵△CAE≌△CBG,
∴∠CBG=∠A=45°,
∴∠GBA=∠GBC+∠CBA=90°,
∵∠BEN+∠BNE=90°,∠BEN+∠CED=90°,
∴∠BNE=∠CED,∵∠EBN=∠CDE=90°,
∴△NBE∽△EDC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴x=1时,y的最大值为 ![]() .
.
(3)解:在CD上取一点K,使得DE=DK=2 ![]() ﹣2,
﹣2,
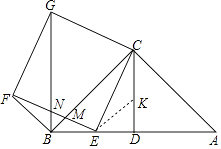
∴EK=4﹣2 ![]() ,
,
∵CK=CD﹣DK=2﹣(2 ![]() ﹣2)=4﹣2
﹣2)=4﹣2 ![]() ,
,
∴KC=EK,
∵∠EKD=∠KED=45°,
∴∠KEC=∠KCE=22.5°,
∴∠CED=67.5°,
∴∠FEB=90°﹣67.5°=22.5°,
∵BE=BD﹣DE=4﹣2 ![]() =EK,CE=EF,∠BEF=∠ECK,
=EK,CE=EF,∠BEF=∠ECK,
∴△BEF≌△KEC,
∴∠EFB=∠ECK=22.5°.
【解析】(1)根据SAS证明即可;(2)只要证明△NBE∽△EDC,可得![]() ,可得
,可得![]() ,由此即可解决问题;(3)在CD上取一点K,使得DE=DK=
,由此即可解决问题;(3)在CD上取一点K,使得DE=DK=![]() ,首先证明KC=EK,再证明△BEF≌△KEC即可解决问题,
,首先证明KC=EK,再证明△BEF≌△KEC即可解决问题,
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意,完成本题解答过程.
(1)解不等式①,得 ,依据是 .
(2)解不等式②,得 .
(3)解不等式③,得 .
(4)把不等式①,②和③的解集在数轴上表示出来.
(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
(6)根据不等式组的解集确立出该不等式组的最大整数解为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+4与反比例函数y= ![]() 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点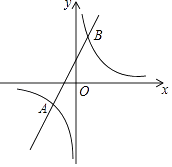
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式 ![]() >x的解集.
>x的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组 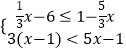 ,下列说法正确的是( )
,下列说法正确的是( )
A.此不等式组的正整数解为1,2,3
B.此不等式组的解集为﹣1<x≤ ![]()
C.此不等式组有5个整数解
D.此不等式组无解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈农科院培育的“黄金8号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
购买种子的数量/kg 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com