
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S四边形CDFE= ![]() S△ABC , 上述结论中始终正确的有( )
S△ABC , 上述结论中始终正确的有( ) 
A.①②③
B.②③④
C.①③④
D.①②④
【答案】C
【解析】解:连接CF, 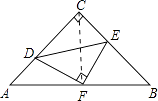
∵AC=BC,∠ACB=90°,点F是AB中点,
∴∠A=∠B=45°,CF⊥AB,∠ACF= ![]() ∠ACB=45°,CF=AF=BF=
∠ACB=45°,CF=AF=BF= ![]() AB,
AB,
∴∠DCF=∠B=45°,
∵∠DFE=90°,
∴∠DFC+∠CFE=∠CFE+∠EFB=90°,
∴∠DFC=∠EFB,
∴△DCF≌△EBF,
∴CD=BE,故①正确;
∴DF=EF,
∴△DFE是等腰直角三角形,故③正确;
∴S△DCF=S△BEF ,
∴S四边形CDFE=S△CDF+S△CEF=S△EBF+S△CEF=S△CBF= ![]() S△ABC , 故④正确.
S△ABC , 故④正确.
若EF⊥BC时,则可得:四边形CDFE是矩形,
∵DF=EF,
∴四边形CDFE是正方形,故②错误.
∴结论中始终正确的有①③④.
故选C.
【考点精析】关于本题考查的等腰直角三角形和三角形的面积,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=﹣ ![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,2)
B.y随x的增大而增大
C.图象在第二、四象限内
D.若x>1,则y>﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与反比例函数y= ![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)点P是x轴上的一动点,试确定点P使PA+PB最小,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点.
x2+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点.
(1)求这个抛物线的解析式;
(2)设P(x,y)是抛物线在第一象限内的一个动点,过点P作直线PH⊥x轴于点H,交直线AB于点M.
①求当x取何值时,PM有最大值?最大值是多少?
②当PM取最大值时,以A、P、M、N为顶点构造平行四边形,求第四个顶点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.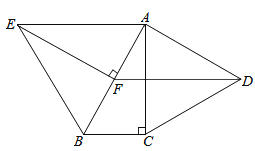
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com