
【题目】在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.” 
(1)若小明同学心里想的是数9,请帮他计算出最后结果: [(9+1)2﹣(9﹣1)2]×25÷9
(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:
甲 | 乙 | 丙 | |
平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?
(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AB的垂直平分线交AC于点N,交BC的延长线于点M,∠A=40°.
(1)求∠NMB的大小.
(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)
(4)将(1)中的∠A改为钝角,对这个问题规律的认识是否需要加以修改?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中AE平分∠BAD交BC于E, ∠CAE=15°,则下面的结论:①△ODC是等边三角形; ②BC=2AB; ③∠AOE=135°; ④![]() ,其中正确结论有( )
,其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm. 
(1)当∠AOB=20°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=20°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm) (参考数据:sin10°≈0.174,cos10°≈0.985,sin20°≈0.342,cos20°≈0.940)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)小宁和婷婷在一起做拼图游戏,他们用 “![]() 、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
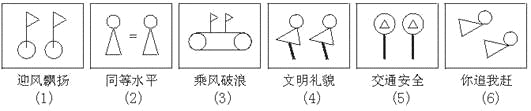
观察以上图案
(1)这个图案有什么特点?
(2)它可以通过一个“基本图案”经过怎样的平移而形成?
(3)在平移的过程中,“基本图案”的大小、形状、位置是否发生了变化?你能解释其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com