
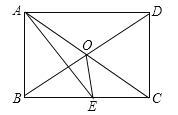
【题目】如图所示,矩形ABCD中AE平分∠BAD交BC于E, ∠CAE=15°,则下面的结论:①△ODC是等边三角形; ②BC=2AB; ③∠AOE=135°; ④![]() ,其中正确结论有( )
,其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=OC,OD=OB,AC=BD,∴OA=OD=OC=OB.∵AE平分∠BAD,∴∠DAE=45°.∵∠CAE=15°,∴∠DAC=30°.∵OA=OD,∴∠ODA=∠DAC=30°,∴∠DOC=60°.∵OD=OC,∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,∴∠DAC=∠ACB=30°,∴AC=2AB.∵AC>BC,∴2AB>BC,∴②错误;
∵AD∥BC,∴∠DBC=∠ADB=30°.∵AE平分∠DAB,∠DAB=90°,∴∠DAE=∠BAE=45°.∵AD∥BC,∴∠DAE=∠AEB,∴∠AEB=∠BAE,∴AB=BE.∵四边形ABCD是矩形,∴∠DOC=60°,DC=AB.∵△DOC是等边三角形,∴DC=OD,∴BE=BO,∴∠BOE=∠BEO=![]() (180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
(180°﹣∠OBE)=75°.∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,∴根据等底等高的三角形面积相等得出S△AOE=SCOE,∴④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】下列代数式:
(1)![]() ; (2)ab÷c2; (3)
; (2)ab÷c2; (3) ![]() ; (4)
; (4) ![]() ; (5)2x(a+b); (6)ab·2.
; (5)2x(a+b); (6)ab·2.
符合代数式书写要求的有几个?答:( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在数学课上,老师提出如下问题: 
小敏的作法如下:
老师说:“小敏的作法正确.”依其作法,先得出ABCD,再得出矩形ABCD,请回答:以上两条结论的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.” 
(1)若小明同学心里想的是数9,请帮他计算出最后结果: [(9+1)2﹣(9﹣1)2]×25÷9
(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等.”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态示范村种植基地计划用90亩~120亩(含90亩与120亩)的土地种植一批葡萄,原计划总产量要达到36万斤.设原计划种植亩数y(亩)、平均亩产量x(万斤)
(1)列出y(亩)与x(万斤)之间的函数关系式,并求自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,四边形
,四边形![]() 是平行四边形,下列结论中错误的是( )
是平行四边形,下列结论中错误的是( )

A. ![]() 以点
以点![]() 为旋转中心,逆时针方向旋转
为旋转中心,逆时针方向旋转![]() 后与
后与![]() 重合
重合
B. ![]() 以点
以点![]() 为旋转中心,顺时针方向旋转
为旋转中心,顺时针方向旋转![]() 后与
后与![]() 重合
重合
C. 沿![]() 所在直线折叠后,
所在直线折叠后,![]() 与
与![]() 重合
重合
D. 沿![]() 所在直线折叠后,
所在直线折叠后,![]() 与
与![]() 重合
重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
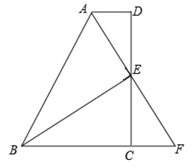
【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com