
如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)①找出图1中的一对全等三角形并说明理由;
②写出图1中线段DE、AD、BE满足的数量关系;(不必说明理由)
(2)当直线MN绕点C旋转到图2的位置时, 探究线段DE、AD、BE之间的数量关系并说明理由;
(3)当直线MN绕点C旋转到图3的位置时,问DE、AD、BE之间又具有怎样的数量关系?直接写出这个数量关系(不必说明理由).

解:(1)①△ADC≌△CEB.
理由如下::∵∠ACB=90°,∠ADC=90°,∠BEC=90°
∴∠ACD+∠DAC=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠BCE,
在△ADC与△BEC中,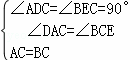 ,
,
∴△ADC≌△BEC(AAS);
②DE=CE+CD=AD+BE.
理由如下:
由①知,△ADC≌△BEC,
∴AD=CE,BE=CD,
∵DE=CE+CD,
∴DE=AD+BE;
(2)∵AD⊥MN于D,BE⊥MN于E.
∴∠ADC=∠BEC=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
在△ADC和△CEB中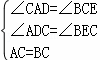 ,
,
∴△ADC≌△CEB.
∴CE=AD,CD=BE.
∴DE=CE﹣CD=AD﹣BE.
(3)同(2),易证△ADC≌△CEB.
∴AD=CE,BE=CD
∵CE=CD﹣ED
∴AD=BE﹣ED,即ED=BE﹣AD;
当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE﹣AD(或AD=BE﹣DE,BE=AD+DE等).


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
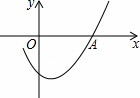
A.b2<4ac B. ac>0 C. 2a﹣b=0 D. a﹣b+c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
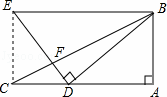
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是 .(将你认为正确的结论的序号都填上)
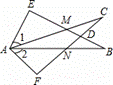
查看答案和解析>>
科目:初中数学 来源: 题型:
将一副直角三角尺BAC和BDE如图放置,其中∠BCA=30°,∠BED=45°,
(1)若∠BFD=75°,判断AC与BE的位置关系,并说明理由;
(2)连接EC,如果AC∥BE,AB∥EC,求∠CED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
小明到超市买练习本,超市正在打折促销:购买10本以上,从第11本开始按标价打折优惠,买练习本所花费的钱数y(元)与练习本的个数x(本)之间的关系如图所示,那么在这个超市买10本以上的练习本优惠折扣是 折.

查看答案和解析>>
科目:初中数学 来源: 题型:
对于反比例函数y= ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(﹣2,﹣1)在它的图象上 B. 它的图象在第一、三象限
C. 当x>0时,y随x的增大而增大 D. 当x<0时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com