
 ��ͼ���ı���ABCD�У�AC=a��BD=b����AC��BD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1����˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2����˽�����ȥ���õ��ı���AnBnCnDn��
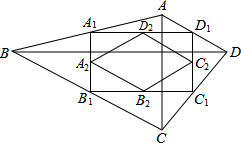
��ͼ���ı���ABCD�У�AC=a��BD=b����AC��BD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1����˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2����˽�����ȥ���õ��ı���AnBnCnDn������ ��1��������������λ�߶����ó�A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC�������ó��ı���A1B1C1D1��ƽ���ı��Σ������þ��ε��ж��ó��𰸣�
��2��ֱ�����þ��ε������Լ�������ε��ж������ó��𰸣�
��3��������������λ�߶����ó��ı���A1B1C1D1�ǵ��ܳ���
��4���������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬�����ó��𰸣�
��� ��1��֤���������ı���ABCD�У�˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1��
��A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC��
��A1D1��B1C1��A1B1��C1D1��
���ı���A1B1C1D1��ƽ���ı��Σ�
��AC�ABD��
���ı���A1B1C1D1�Ǿ��Σ�
��2���⣺���ı���A1B1C1D1�Ǿ��Σ�
��B1D1=A1C1�����ε������Խ�����ȣ���
��A2D2=C2D2=C2B2=B2A2����λ�߶�������
���ı���A2B2C2D2�����Σ�
���ı���A3B3C3D3�Ǿ��Σ�
�ʴ�Ϊ���أ�
��3���⣺������������λ�߶����ɵ�D1C1=A1B1=$\frac{1}{2}$AC=$\frac{1}{2}$a��A1D1=B1C1=$\frac{1}{2}$BC=$\frac{1}{2}$b�����ı���A1B1C1D1�ǵ��ܳ�Ϊa+b��
�ʴ�Ϊ��a+b��
��4���⣺���ı���ABCD�У�AC=a��BD=b����AC�ABD��
��S�ı���ABCD=ab��2��
�������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬
�ı���AnBnCnDn�������$\frac{ab}{{2}^{n+1}}$��
�ʴ�Ϊ��$\frac{ab}{{2}^{n+1}}$��
���� ������Ҫ�������е��ı����Լ���������λ�߶�������ȷ���վ����Լ����ε��ж������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
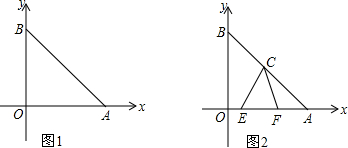
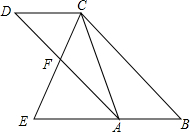 ��ͼ����֪���ı���ABCD��ƽ���ı��Σ���E�ڱ�BA���ӳ����ϣ�CE��AD�ڵ�F����ECA=��D
��ͼ����֪���ı���ABCD��ƽ���ı��Σ���E�ڱ�BA���ӳ����ϣ�CE��AD�ڵ�F����ECA=��D�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ���ı���ABCD�Ķ���C��y���������ϣ�CDƽ����x�ᣬֱ��AC��x���ڵ�E��BC��AC������BE������������y=$\frac{k}{x}$��x��0����ͼ����D����֪S��BCE=2����k��ֵ��4��
��ͼ��ƽ���ı���ABCD�Ķ���C��y���������ϣ�CDƽ����x�ᣬֱ��AC��x���ڵ�E��BC��AC������BE������������y=$\frac{k}{x}$��x��0����ͼ����D����֪S��BCE=2����k��ֵ��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=$\frac{1}{2}{x}^{2}$+��m-2��x+2m-6�ĶԳ���Ϊֱ��x=1����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��֪������y=$\frac{1}{2}{x}^{2}$+��m-2��x+2m-6�ĶԳ���Ϊֱ��x=1����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
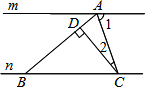 ��ͼ��ֱ��m��n����A��ֱ��m�ϣ���B��C��ֱ��n�ϣ�AB=BC����1=70�㣬CD��AB��D����ô��2���ڣ�������
��ͼ��ֱ��m��n����A��ֱ��m�ϣ���B��C��ֱ��n�ϣ�AB=BC����1=70�㣬CD��AB��D����ô��2���ڣ�������| A�� | 20�� | B�� | 30�� | C�� | 32�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com