
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
(1)求代数式mn的值;
(2)若二次函数![]() 的图象经过点B,求代数式
的图象经过点B,求代数式![]() 的值;
的值;
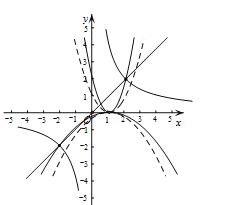
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象只有一个交点,且该交点在直线
的图象只有一个交点,且该交点在直线![]() 的下方,结合函数图象,求
的下方,结合函数图象,求![]() 的取值范围.
的取值范围.

【答案】(1)4;(2)8;(3)![]() 或
或![]() .
.
【解析】
试题(1)由A的坐标求出k的值,再把B的坐标代入反比例函数即可求出mn的值;
(2)把![]() 代入二次函数
代入二次函数![]() ,可得
,可得![]() ,即
,即![]() ,再由
,再由![]() ,原式可变形为
,原式可变形为![]() ,即可求出表达式的值;
,即可求出表达式的值;
(3)先求出反比例函数与直线![]() 的两个交点
的两个交点![]() ,
, ![]() ,再结合图象可得出结论.
,再结合图象可得出结论.
试题解析:(1)∵反比例函数![]() 的图象经过点
的图象经过点![]() ,∴
,∴![]() ,∴反比例函数的解析式为
,∴反比例函数的解析式为![]() ,∵反比例函数
,∵反比例函数![]() 的图象经过点
的图象经过点![]() ,∴
,∴![]() ;
;
(2)∵二次函数![]() 的图象经过点
的图象经过点![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,由(1)得
,由(1)得![]() ,∴原式-
,∴原式-![]() ;
;
(3)由(1)得反比例函数的解析式为![]() .令
.令![]() ,可得
,可得![]() ,解得
,解得![]() .∴反比例函数
.∴反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,
, ![]() .当二次函数
.当二次函数![]() 的图象经过点
的图象经过点![]() 时,可得
时,可得![]() ;
;
当二次函数![]() 的图象经过点
的图象经过点![]() 时,可得
时,可得![]() .
.
∵二次函数![]() 的顶点为
的顶点为![]() ,∴由图象可知,符合题意的
,∴由图象可知,符合题意的![]() 的取值范围是
的取值范围是![]() 或
或![]() .(注:只写
.(注:只写![]() 或只写
或只写![]() ,减1分.)
,减1分.)


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
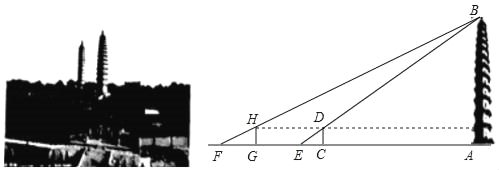
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
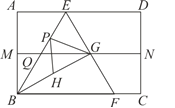
【题目】如图,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,把纸片
,把纸片![]() 对折,折痕为
对折,折痕为![]() ,展开后再过点
,展开后再过点![]() 折叠该纸片,使点
折叠该纸片,使点![]() 落在
落在![]() 上的点
上的点![]() 处,且折痕
处,且折痕![]() 与
与![]() 相交于点
相交于点![]() ,再次展平后,连接
,再次展平后,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() ,
,![]() 的长;
的长;
(3)![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是 .(请直接写出结果)
的最小值是 .(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
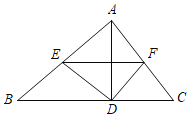
【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=12,AC=9,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
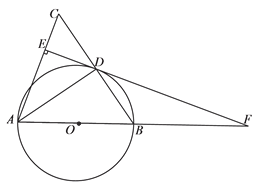
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
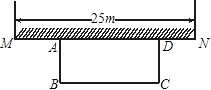
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
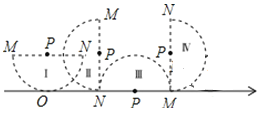
【题目】如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅳ,其中位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上.
解答下列问题:
(1)位置Ⅰ中的MN与数轴之间的距离为____________;
(2)位置Ⅱ中的半⊙P与数轴的位置关系是________;
(3)求位置Ⅲ中的圆心P在数轴上表示的数;
(4)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求该纸片所扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
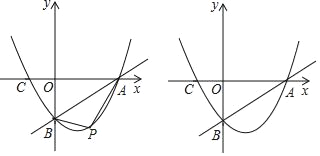
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
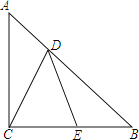
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC,连DE、CD.
(1)找出图中全等图形,并证明;
(2)求∠ACD的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com