
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ����
����![]() ���������ϣ�
���������ϣ�
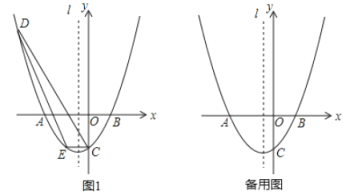
��1����ͼ1��![]() Ϊֱ��
Ϊֱ��![]() �·��������ϵ�һ�㣬����
�·��������ϵ�һ�㣬����![]() ��
��![]() ����
����![]() ��������ʱ����ֱ��
��������ʱ����ֱ��![]() ��ȡһ��
��ȡһ��![]() ����
����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ��
��Ĵ��ߣ�����Ϊ��![]() ������
������![]() ��
��![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����������![]() ��
��![]() ��������ƽ�Ƶõ���������
��������ƽ�Ƶõ���������![]() ��
��![]() ����ԭ��
����ԭ��![]() ��
��![]() ��
��![]() �����һ������Ϊ
�����һ������Ϊ![]() ����
����![]() ��������
��������![]() ������һ�㣬��
������һ�㣬��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ܷ��Ϊ�Ե�
�ܷ��Ϊ�Ե�![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ����ܡ�ֱ��д����
Ϊֱ�Ƕ���ĵ���ֱ�������Σ����ܡ�ֱ��д����![]() �����꣬�����ܣ���˵�����ɣ�
�����꣬�����ܣ���˵�����ɣ�
���𰸡���1��![]() ��2���ܣ�P�������Ϊ��
��2���ܣ�P�������Ϊ�� ��
��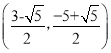 ��
��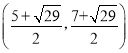 ��
��
��������
(1) ����������¡�C�� D�������꣬���ô���ϵ�������ֱ��CD��ֱ�߷��̣���ͼ1�У�����E��EG //y�ύֱ��CD��G����E (m,![]() +2m-3)����G (m,-2m-3)��GE=-
+2m-3)����G (m,-2m-3)��GE=-![]() -4m������S��EDC=
-4m������S��EDC=![]() ��EG��|DX|=
��EG��|DX|=![]() (-
(-![]() -4m) ��4=-2
-4m) ��4=-2![]() +8����֪m=-2ʱ����DEC��������ʱE(-2, -3) ����֤��Rt��EHM��Rt��BON���ɽ�����⣻
+8����֪m=-2ʱ����DEC��������ʱE(-2, -3) ����֤��Rt��EHM��Rt��BON���ɽ�����⣻
��2���������.��ͼ2��.��P M��x����M��P N�ͶԳ���|��N���Գ���l|��0A��K������PMF�ա�PNQ���Ƴ�PM=PN���Ƴ���P�ڡ�MKN�Ľ�ƽ�����ϣ�ֻҪ���ֱ��KP�Ľ���ʽ�����������鼴�����P��P�����꣬ͬ������P�� P4�����꣮
�⣺��1��������A(1,0)��B(-3,0)��C(0,-3)��D(-4,5)��
��ֱ��CD�Ľ���ʽΪy= kx+b,����
b=-3��-4k+b=5 ��k=-2��b=-3
��ֱ��CD�Ľ���ʽΪy=-2x-3
��ͼ1�У�����E��EG��y�ύֱ��CD��G����E(m,![]() +2m-3)����G(m,-2m-3)
+2m-3)����G(m,-2m-3)
��GE=-m-4m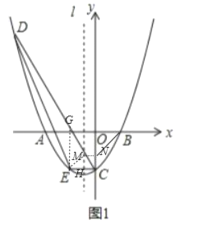
��S��EDC=![]() ��EG��|DX|=
��EG��|DX|=![]() (-
(-![]() -4m) ��4=-2
-4m) ��4=-2![]() +8��
+8��
��-2��0����m=-2ʱ����DEC��������ʱE(-2,-3)��
��C(0,-3)��
��EC��AB����CE���Գ�����H����B(1,0)��
��EH=OB=1��
��EM=BN��
��Rt��EHM��Rt��BON��
��MH=ON=![]() OC=
OC=![]()
��EM=BN=![]() ��
��
��EM+MN+MB=![]()
��2��������������ĵ㣬��ͼ2����PM��x����M��PN�ͶԳ���l��N���Գ���l��OA��K��
��PQ=PF����QPF=90�㣬��NQP =��MFP ���ɵá�PMF�ա�PNQ
��PM=PN�����P�ڡ�MKN�Ľ�ƽ�����ϣ�
��ֱ��KP��(-1,0)����x���45��ǣ����������������ޣ�
��ֱ��KP�Ľ���ʽΪy=-x-1��
������������ƽ���� 3����λ��
��������y�Ľ���ʽΪy=x-4x��
��P ��������y��ֱ��KP �Ľ���
��![]()
���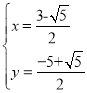 ��
��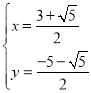
��P ��P
��P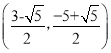

ͬ����֪��ֱ��y=x+1�������ߵĽ���P3��P4����������
��![]()
���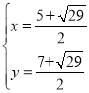 ��
��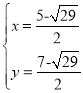
��P3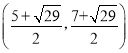
P4
�������������������ĵ�P����Ϊ��
 ��
��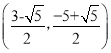 ��
��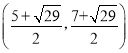 ��
��


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
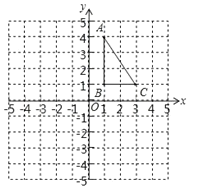
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������������ֱ�ΪA(1��4)��B(1��1)��C(3��1)��
��1��������ABC����ԭ������ĶԳƵġ�A1B1C1����д����C1�����ꣻ
��2����ABC���ŵ�B��ʱ����ת90����������ת���Ӧ�ġ�A2BC2����д����A2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016���������У���ͼ�����߶�AB�Ƶ�O˳ʱ����ת90���õ��߶�A��B������ôA����2��5���Ķ�Ӧ��A���������ǣ�������

A. ��2��5�� B. ��5��2�� C. ��2����5�� D. ��5����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������BAC=������D�ڱ�AC�ϣ������A��C�غϣ�����BD����KΪ�߶�BD���е㣬����D��DE��AB�ڵ�E������CK��EK��CE������ADE�Ƶ�A˳ʱ����תһ���ĽǶȣ���ת��С��90����

��1����ͼ1������=45��������ECK����״Ϊ______��
��2���ڣ�1���������£�����ͼ1�е���ADE�Ƶ�A��ת��ʹ��D��E��B���㹲�ߣ���KΪ�߶�BD���е㣬��ͼ2��ʾ����֤��BE-AE=2CK��
��3������ADE�Ƶ�A��ת��ͼ3λ��ʱ��ʹ��D��E��B���㹲�ߣ���K��Ϊ�߶�BD���е㣬����ֱ��д��BE��AE��CK����֮���������ϵ���ú��������Ǻ�����ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵ��������Σ�
�ǵ��������Σ�![]() ����
����![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ��
��
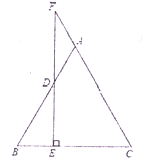
��1��֤����![]() �ǵ��������Σ�
�ǵ��������Σ�
��2����![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������깺���֧����ʽ�������࣬ij��ѧ��ȤС��ʹ˽����˳������飮��������ʾ��֧����ʽ�У�A�š�B֧������C�ֽ�D��������С���ij����һ���ڹ����ߵ�֧����ʽ���е���ͳ�ƣ��õ�����������������ͳ��ͼ��

�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1������һ�������˶����������ߣ�
��2���벹ȫ����ͳ��ͼ��������ͳ��ͼ��A��֧����ʽ����Ӧ��Բ�Ľ�Ϊ�� ���ȣ�
��3�����ó�����һ������1600�������ߣ��������ʹ��A��B����֧����ʽ�Ĺ����߹��ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ij�������������������������ɱ�Ϊ30Ԫ/����ÿ������y�����������۵���x��Ԫ��֮�����һ�κ�����ϵ������40Ԫÿ������ʱ��ÿ�������300��������55Ԫÿ������ʱ��ÿ�������150����
��1����y��x֮��ĺ�����ϵʽ��
��2������涨ÿ��������������������������240���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
��3���õ����������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3600Ԫ����ֱ��д�����������������۵��۵ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
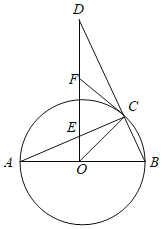
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����O��OD��AB����BC���ӳ�����D����AC�ڵ�E��F��DE���е㣬����CF��
��1����֤��CF�ǡ�O�����ߣ�
��2������A��22.5������֤��CE��CB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BA��BC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E��BC���ӳ����ڡ�O������AF���ڵ�F��
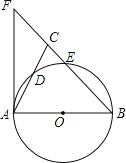
��1����֤����ABC��2��CAF��
��2����AC��2![]() ��CE��EB��1��4����CE�ij���
��CE��EB��1��4����CE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com