
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(﹣1,4).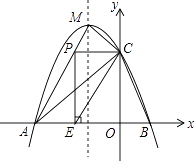
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD与△ACB面积相等时,求点D的坐标;
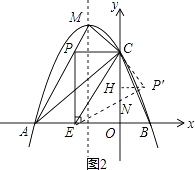
(3)点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将△PCE沿直线CE翻折,使点P的对应点P′与P、E、C处在同一平面内,请求出点P′坐标,并判断点P′是否在该抛物线上.
【答案】
(1)
解:∵抛物线y=ax2+bx+c经过点C(0,3),顶点为M(﹣1,4),
∴ 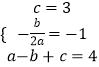 ,解得:
,解得: 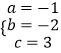 .
.
∴所求抛物线的解析式为y=﹣x2﹣2x+3
(2)
解:依照题意画出图形,如图1所示.
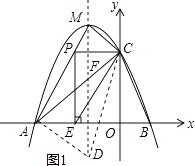
令y=﹣x2﹣2x+3=0,解得:x=﹣3或x=1,
故A(﹣3,0),B(1,0),
∴OA=OC,△AOC为等腰直角三角形.
设AC交对称轴x=﹣1于F(﹣1,yF),
由点A(﹣3,0)、C(0,3)可知直线AC的解析式为y=x+3,
∴yF=﹣1+3=2,即F(﹣1,2).
设点D坐标为(﹣1,yD),
则S△ADC= ![]() DFAO=
DFAO= ![]() ×|yD﹣2|×3.
×|yD﹣2|×3.
又∵S△ABC= ![]() ABOC=
ABOC= ![]() ×[1﹣(﹣3)]×3=6,且S△ADC=S△ABC,
×[1﹣(﹣3)]×3=6,且S△ADC=S△ABC,
∴ ![]() ×|yD﹣2|×3.=6,解得:yD=﹣2或yD=6.
×|yD﹣2|×3.=6,解得:yD=﹣2或yD=6.
∴点D的坐标为(﹣1,﹣2)或(﹣1,6)
(3)
解:如图2,点P′为点P关于直线CE的对称点,过点P′作PH⊥y轴于H,设P′E交y轴于点N.
在△EON和△CP′N中, 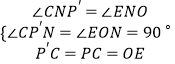 ,
,
∴△EON≌△CP′N(AAS).
设NC=m,则NE=m,
∵A(﹣3,0)、M(﹣1,4)可知直线AM的解析式为y=2x+6,
∴当y=3时,x=﹣ ![]() ,即点P(﹣
,即点P(﹣ ![]() ,3).
,3).
∴P′C=PC= ![]() ,P′N=3﹣m,
,P′N=3﹣m,
在Rt△P′NC中,由勾股定理,得: ![]() +(3﹣m)2=m2,
+(3﹣m)2=m2,
解得:m= ![]() .
.
∵S△P′NC= ![]() CNP′H=
CNP′H= ![]() P′NP′C,
P′NP′C,
∴P′H= ![]() .
.
由△CHP′∽△CP′N可得: ![]() ,
,
∴CH= ![]() =
= ![]() ,
,
∴OH=3﹣ ![]() =
= ![]() ,
,
∴P′的坐标为( ![]() ,
, ![]() ).
).
将点P′( ![]() ,
, ![]() )代入抛物线解析式,
)代入抛物线解析式,
得:y=﹣ ![]() ﹣2×
﹣2× ![]() +3=
+3= ![]() ≠
≠ ![]() ,
,
∴点P′不在该抛物线上.
【解析】(1)由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;(2)设点D坐标为(﹣1,yD),根据三角形的面积公式以及△ACD与△ACB面积相等,即可得出关于yD含绝对值符号的一元一次方程,解方程即可得出结论;(3)作点P关于直线CE的对称点P′,过点P′作PH⊥y轴于H,设P′E交y轴于点N.根据对称的性质即可得出△EON≌△CP′N,从而得出CN=NE,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标,在Rt△P′NC中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点P′的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:

(2)原正方形能否被分割成2018个三角形?若能,求此时正方形ABCD内部有多少个点;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y= ![]() (k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为
(k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为 ![]() ,点C横坐标为1.
,点C横坐标为1. 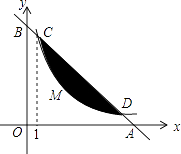
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成 ![]() 个扇形,如图)并规定:顾客在本商场每消费
个扇形,如图)并规定:顾客在本商场每消费 ![]() 元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?
元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+a﹣c=0,其中a、b、c分别为△ABC三边的长.下列关于这个方程的解和△ABC形状判断的结论错误的是( )
A. 如果x=﹣1是方程的根,则△ABC是等腰三角形
B. 如果方程有两个相等的实数根,则△ABC是直角三角形
C. 如果△ABC是等边三角形,方程的解是x=0或x=﹣1
D. 如果方程无实数解,则△ABC是锐角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.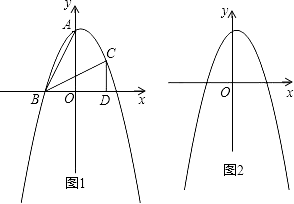
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com