练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：（ ）﹣2+（ ﹣ ）0+| ﹣1|+（ ﹣3 ）tan60°．

    【答案】解：原式=9+1+ ﹣1+（2 ﹣3 ） =9+ ﹣3
    =6+
    【解析】利用负整数指数幂、零指数幂、绝对值的意义和特殊角的三角函数值得到原式=9+1+ ﹣1+（2 ﹣3 ） ，然后进行二次根式的乘法运算后合并即可．
    【考点精析】利用零指数幂法则和整数指数幂的运算性质对题目进行判断即可得到答案，需要熟知零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C（0，3），且此抛物线的顶点坐标为M（﹣1，4）．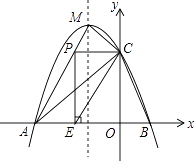

    （1）求此抛物线的解析式；
    （2）设点D为已知抛物线对称轴上的任意一点，当△ACD与△ACB面积相等时，求点D的坐标；
    （3）点P在线段AM上，当PC与y轴垂直时，过点P作x轴的垂线，垂足为E，将△PCE沿直线CE翻折，使点P的对应点P′与P、E、C处在同一平面内，请求出点P′坐标，并判断点P′是否在该抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某生物兴趣小组在四天的实验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同．他们将一头骆驼前两昼夜的体温变化情况绘制成下图．请根据图像回答问题：

    (1)第一天中，在什么时间范围内这头骆驼的体温是上升的？它的体温从最低上升到最高需要多少时间？

    (2)第三天12时这头骆驼的体温约是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下图是由一些火柴棒搭成的图案：

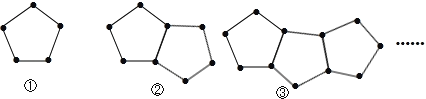
    （1）摆第①个图案用 根火柴棒，摆第②个图案用 根火柴棒，摆第③个图案用 根火柴棒．

    （2）按照这种方式摆下去，摆第n个图案用多少根火柴棒？

    （3）计算一下摆121根火柴棒时，是第几个图案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

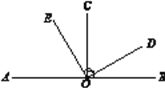
    【题目】如果两个锐角的和等于90°，那么我们就称这两个角互为余角．类似可以定义：如果两个角的差的绝对值等于90°，那么我们就可以称这两个角互为垂角．例如：∠1＝120°，∠2＝30°，|∠1－∠2|＝90°，则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)．

    (1)如图，O为直线AB上一点，OC⊥AB于点O，OE⊥OD于点O ，请写出图中所有互为垂角的角：_______________________________________________________；

    (2)如果一个角的垂角等于这个角的补角的，求这个角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】节能电动车越来越受到人们的喜欢，新开发的各种品牌电动车相继投入市场．小李车行经营的A型节能电动车2015年销售总额为m万元，2016年每辆A型节能电动车的销售价比2015年降低2000年，若2015年和2016年卖出的节能电动车的数量相同（同一型号的节能电动车每辆的销售价格相同），则2016年的销售总额比2015年减少20%．
    （1）2016年A型节能电动车每辆售价多少万元？（用列方程方法解答）
    （2）小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车，每购进3辆节能电动车，批发商就给车行返回1500元．若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍，全部销售获得的利润不少于18万元，且2016年A，B两种型号节能电动车的进货和销售价格如表，那么2016年新款B型节能电动车至少要购进多少辆？

    A型节能电动车

    B型节能电动车

    进货价格（万元/辆）

    0.55

    0.7

    销售价格（万元/辆）

    2016年的销售价格

    2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=4 ，则S阴影=（ ）
    A.2π??
    B. π??
    C. π??
    D. π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

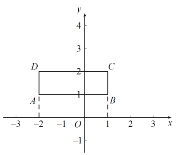
    【题目】如图，在平面直角坐标系xOy中，长方形ABCD的四个顶点分别为（1，1），（1，2），（-2，2），（-2，1）.对该长方形及其内部的每一个点都进行如下操作：把每个点的横坐标都乘以同一个实数a，纵坐标都乘以3，再将得到的点向右平移m（m＞0）个单位，向下平移2个单位，得到长方形ABCD及其内部的点，其中点A，B，C，D的对应点分别为A，B，C，D.

    （1）点A的横坐标为__________（用含a,m的式子表示）.

    （2）点A的坐标为（3，1），点C的坐标为（-3，4），

    ①求a，m的值；

    ②若对长方形ABCD内部（不包括边界）的点E(0，y)进行上述操作后，得到的对应点E仍然在长方形ABCD内部（不包括边界），求y的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=ax2+b的顶点坐标为（0，﹣1），且经过点A（﹣2，0）．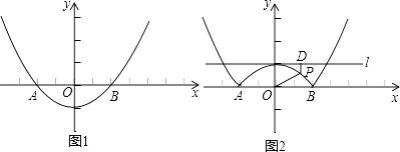
    （1）求抛物线的解析式；
    （2）若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方，x轴上方的图象保持不变，就得到了函数y=|ax2+b|图象上的任意一点P，直线l是经过（0，1）且平行与x轴的直线，过点P作直线l的垂线，垂足为D，猜想并探究：PO与PD的差是否为定值？如果是，请求出此定值；如果不是，请说明理由． （注：在解题过程中，如果你觉得有困难，可以阅读下面的材料）
    附阅读材料：
    ① 在平面直角坐标系中，若A、B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），则A，B两点间的距离为|AB|= ，这个公式叫两点间距离公式．
    例如：已知A，B两点的坐标分别为（﹣1，2），（2，﹣2），则A，B两点间的距离为|AB|= =5．
    ② 因式分解：x4+2x2y2+y4=（x2+y2）2 ．

    查看答案和解析>>

    同步练习册答案