Question

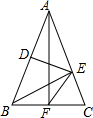
17．如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则下面结论错误的是（　　）

• A． BF=EF
• B． DE=EF
• C． ∠EFC=45°
• D． ∠BEF=∠CBE

Answer 1

分析 根据等腰三角形的三线合一得到BF=FC，根据直角三角形的性质判断A；根据直角三角形的性质判断B；根据三角形内角和定理和等腰三角形的性质判断C，根据直角三角形的性质判断D．

解答 解：∵AB=AC，AF⊥BC，
∴BF=FC，
∵BE⊥AC，
∴EF=$\frac{1}{2}$BC=BF，A不合题意；
∵DE=$\frac{1}{2}$AB，EF=$\frac{1}{2}$BC，不能证明DE=EF，B符合题意；
∵DE垂直平分AB，
∴EA=EB，又BE⊥AC，
∴∠BAC=45°，
∴∠C=67.5°，又FE=FC，
∴∠EFC=45°，C不合题意；
∵FE=FB，
∴∠BEF=∠CBE；
故选：B．

点评 本题考查的是线段垂直平分线的性质、等腰三角形的性质和直角三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．